1.「2025辽宁沈阳期中」下列方程是关于x的一元二次方程的是 (
A. $ a x ^ { 2 } + b x + c = 0 $
B. $ \frac { 1 } { x ^ { 2 } } + \frac { 1 } { x } = 2 $
C. $ y ^ { 2 } + 2 x = - 1 $
D. $ 3 ( x + 1 ) ^ { 2 } = 2 ( x + 1 ) $
D
)A. $ a x ^ { 2 } + b x + c = 0 $
B. $ \frac { 1 } { x ^ { 2 } } + \frac { 1 } { x } = 2 $
C. $ y ^ { 2 } + 2 x = - 1 $
D. $ 3 ( x + 1 ) ^ { 2 } = 2 ( x + 1 ) $
答案:D A. 当 $ a = 0 $ 时,原方程不是一元二次方程;B. 方程 $ \frac{1}{x^{2}}+\frac{1}{x}=2 $ 中含有分式,不是一元二次方程;C. $ y^{2}+2x=-1 $ 中含有 2 个未知数,不是一元二次方程;D. $ 3(x + 1)^{2}=2(x + 1) $,整理得 $ 3x^{2}+4x + 1 = 0 $,是一元二次方程. 故选 D.
2.「2024河北秦皇岛卢龙期中」方程 $ k x ^ { 2 } + 3 x = x ^ { 2 } + 5 $ 是关于x的一元二次方程,则k的取值范围是 (
A. $ k \neq 0 $
B. $ k \neq - 1 $
C. $ k \neq 1 $
D. $ k \neq \pm 1 $
C
)A. $ k \neq 0 $
B. $ k \neq - 1 $
C. $ k \neq 1 $
D. $ k \neq \pm 1 $
答案:C 原方程化为一般形式为 $ (k - 1)x^{2}+3x - 5 = 0 $,∵ 方程 $ kx^{2}+3x = x^{2}+5 $ 是关于 $ x $ 的一元二次方程,∴ $ k - 1 \neq 0 $,解得 $ k \neq 1 $. 故选 C.
3.「2025河北定州期中」将方程 $ 5 x ^ { 2 } - x = 7 x $ 化为一般形式后,二次项系数、一次项系数、常数项分别是 (
A. 5,7,-1
B. -5,7,1
C. 5,-7,-1
D. 5,-8,0
D
)A. 5,7,-1
B. -5,7,1
C. 5,-7,-1
D. 5,-8,0
答案:D ∵ 方程 $ 5x^{2}-x = 7x $ 化成一般形式是 $ 5x^{2}-8x = 0 $,∴ 二次项系数、一次项系数和常数项分别为 $ 5 $,$ -8 $,$ 0 $. 故选 D.
4.「2024广东深圳南山模拟」若关于x的方程 $ m x ^ { 3 } + 2 x ^ { n } - 3 x + 1 = 0 $ 是一元二次方程,则 $ m + n = $
2
.答案:答案 2
解析 ∵ 关于 $ x $ 的方程 $ mx^{3}+2x^{n}-3x + 1 = 0 $ 是一元二次方程,∴ $ m = 0 $,$ n = 2 $,∴ $ m + n = 2 $.
解析 ∵ 关于 $ x $ 的方程 $ mx^{3}+2x^{n}-3x + 1 = 0 $ 是一元二次方程,∴ $ m = 0 $,$ n = 2 $,∴ $ m + n = 2 $.
5.「2025湖南娄底娄星期中」若关于x的一元二次方程 $ ( m - 1 ) x ^ { 2 } + x + m ^ { 2 } - 1 = 0 $ 的常数项为0,则m的值是____
-1
.答案:答案 -1
解析 ∵ 一元二次方程 $ (m - 1)x^{2}+x + m^{2}-1 = 0 $ 的常数项为 0,∴ $ \begin{cases}m - 1 \neq 0,\\m^{2}-1 = 0,\end{cases} $ 解得 $ m = -1 $.
解析 ∵ 一元二次方程 $ (m - 1)x^{2}+x + m^{2}-1 = 0 $ 的常数项为 0,∴ $ \begin{cases}m - 1 \neq 0,\\m^{2}-1 = 0,\end{cases} $ 解得 $ m = -1 $.
6. 把下列方程化为一元二次方程的一般形式,并写出其中的二次项系数、一次项系数和常数项.
(1) $ 2 x ^ { 2 } = 1 - 3 x $.
一般形式为
(2) $ 5 x ( x - 2 ) = 4 x ^ { 2 } - 3 x $.
一般形式为
(1) $ 2 x ^ { 2 } = 1 - 3 x $.
一般形式为
$2x^{2}+3x - 1 = 0$
,二次项系数为2
,一次项系数为3
,常数项为-1
.(2) $ 5 x ( x - 2 ) = 4 x ^ { 2 } - 3 x $.
一般形式为
$x^{2}-7x = 0$
,二次项系数为1
,一次项系数为-7
,常数项为0
.答案:解析 (1) 方程 $ 2x^{2}=1 - 3x $ 化成一般形式为 $ 2x^{2}+3x - 1 = 0 $,二次项系数为 2,一次项系数为 3,常数项为 -1.
(2) 方程 $ 5x(x - 2)=4x^{2}-3x $ 化成一般形式为 $ x^{2}-7x = 0 $,二次项系数为 1,一次项系数为 -7,常数项为 0.
(2) 方程 $ 5x(x - 2)=4x^{2}-3x $ 化成一般形式为 $ x^{2}-7x = 0 $,二次项系数为 1,一次项系数为 -7,常数项为 0.
7.「2025广东河源龙川期中」若关于x的方程 $ x ^ { 2 } - k x - 4 = 0 $ 有一个根为-1,则k的值为 (
A. -4
B. -3
C. 3
D. 4
C
)A. -4
B. -3
C. 3
D. 4
答案:C 把 $ x = -1 $ 代入方程 $ x^{2}-kx - 4 = 0 $ 得 $ 1 + k - 4 = 0 $,解得 $ k = 3 $. 故选 C.
8.「2024广东深圳中考」一元二次方程 $ x ^ { 2 } - 3 x + a = 0 $ 的一个解为 $ x = 1 $,则 $ a = $
2
.答案:答案 2
解析 将 $ x = 1 $ 代入一元二次方程得 $ 1 - 3 + a = 0 $,解得 $ a = 2 $.
解析 将 $ x = 1 $ 代入一元二次方程得 $ 1 - 3 + a = 0 $,解得 $ a = 2 $.
9.「2024四川南充中考」已知m是方程 $ x ^ { 2 } + 4 x - 1 = 0 $ 的一个根,则 $ ( m + 5 ) ( m - 1 ) $ 的值为
-4
.答案:答案 -4
解析 把 $ x = m $ 代入 $ x^{2}+4x - 1 = 0 $,得 $ m^{2}+4m - 1 = 0 $,∴ $ m^{2}+4m = 1 $,∴ $ (m + 5)(m - 1)=m^{2}-m + 5m - 5 = m^{2}+4m - 5 = 1 - 5 = -4 $.
解析 把 $ x = m $ 代入 $ x^{2}+4x - 1 = 0 $,得 $ m^{2}+4m - 1 = 0 $,∴ $ m^{2}+4m = 1 $,∴ $ (m + 5)(m - 1)=m^{2}-m + 5m - 5 = m^{2}+4m - 5 = 1 - 5 = -4 $.
10. (1) 填表:
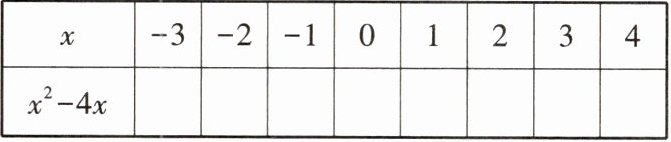
(2) 观察表格,哪些数是一元二次方程 $ x ^ { 2 } - 4 x = - 3 $ 的根?

| $ x $ | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 |
| ---- | ---- | ---- | ---- | ---- | ---- | ---- | ---- | ---- |
| $ x^{2}-4x $ | 21 | 12 | 5 | 0 | -3 | -4 | -3 | 0 |
| ---- | ---- | ---- | ---- | ---- | ---- | ---- | ---- | ---- |
| $ x^{2}-4x $ | 21 | 12 | 5 | 0 | -3 | -4 | -3 | 0 |
(2) 观察表格,哪些数是一元二次方程 $ x ^ { 2 } - 4 x = - 3 $ 的根?
1和3
答案:解析 (1) 填表如下:
| $ x $ | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 |
| ---- | ---- | ---- | ---- | ---- | ---- | ---- | ---- | ---- |
| $ x^{2}-4x $ | 21 | 12 | 5 | 0 | -3 | -4 | -3 | 0 |
(2) 观察表格可知,当 $ x = 1 $ 或 $ x = 3 $ 时,$ x^{2}-4x = -3 $,所以 1 和 3 是方程 $ x^{2}-4x = -3 $ 的根.
| $ x $ | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 |
| ---- | ---- | ---- | ---- | ---- | ---- | ---- | ---- | ---- |
| $ x^{2}-4x $ | 21 | 12 | 5 | 0 | -3 | -4 | -3 | 0 |
(2) 观察表格可知,当 $ x = 1 $ 或 $ x = 3 $ 时,$ x^{2}-4x = -3 $,所以 1 和 3 是方程 $ x^{2}-4x = -3 $ 的根.
11.「2025山西太原迎泽月考」要组织一场篮球联赛,每两队之间只赛一场,计划安排15场比赛,如果邀请x个球队参加比赛,根据题意,列出方程为 (
A. $ x ( x - 1 ) = 15 $
B. $ x ( x + 1 ) = 15 $
C. $ \frac { x ( x - 1 ) } { 2 } = 15 $
D. $ \frac { x ( x + 1 ) } { 2 } = 15 $
C
)A. $ x ( x - 1 ) = 15 $
B. $ x ( x + 1 ) = 15 $
C. $ \frac { x ( x - 1 ) } { 2 } = 15 $
D. $ \frac { x ( x + 1 ) } { 2 } = 15 $
答案:C 邀请 $ x $ 个球队参加比赛,每两队之间只赛一场,每个队都与其他 $ (x - 1) $ 个球队赛一场,所以全部比赛共 $ \frac{x(x - 1)}{2} $ 场,列方程为 $ \frac{x(x - 1)}{2}=15 $. 故选 C.
12.「2024重庆沙坪坝期中」某公园计划在一块长为10米,宽为8米的矩形草坪中央划分出一块30平方米的矩形区域作为宠物乐园,若宠物乐园四周草坪的宽度都一样,记为x米,根据题意,可列出方程为
(8 - 2x)(10 - 2x)=30
.(不化简,不解答)答案:答案 $ (8 - 2x)(10 - 2x)=30 $
解析 由题意可知中央矩形区域的长为 $ (10 - 2x) $ 米,宽为 $ (8 - 2x) $ 米,则根据矩形面积公式可列方程为 $ (8 - 2x)(10 - 2x)=30 $.
解析 由题意可知中央矩形区域的长为 $ (10 - 2x) $ 米,宽为 $ (8 - 2x) $ 米,则根据矩形面积公式可列方程为 $ (8 - 2x)(10 - 2x)=30 $.