3.「2024 山西中考」综合与实践
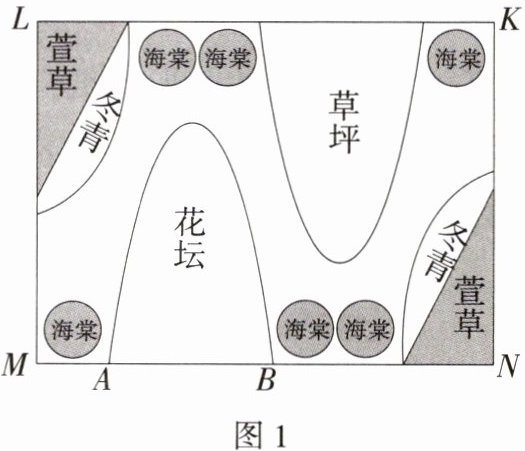
问题情境:如图 1,矩形$MNKL$是学校花园的示意图,其中一个花坛的轮廓可近似看成由抛物线的一部分与线段$AB$组成的封闭图形,点$A$,$B在矩形的边MN$上.现要对该花坛内种植区域进行划分,以种植不同花卉,学校面向全体同学征集设计方案.
方案设计:如图 2,$AB = 6$米,$AB的垂直平分线与抛物线交于点P$,与$AB交于点O$,点$P$是抛物线的顶点,且$PO = 9$米.欣欣设计的方案如下:
第一步:在线段$OP上确定点C$,使$∠ACB = 90^{\circ}$.用篱笆沿线段$AC$,$BC分隔出△ABC$区域,种植串串红;
第二步:在线段$CP上取点F$(不与$C$,$P$重合),过点$F作AB$的平行线,交抛物线于点$D$,$E$.用篱笆沿$DE$,$CF将线段AC$,$BC$与抛物线围成的区域分隔成三部分,分别种植不同花色的月季.

方案实施:学校采用了欣欣的方案,在完成第一步$△ABC$区域的分隔后,发现仅剩 6 米篱笆材料.若要在第二步分隔中恰好用完 6 米材料,需确定$DE与CF$的长.为此,欣欣在图 2 中以$AB所在直线为x$轴,$OP所在直线为y$轴建立平面直角坐标系.请按照她的方法解决问题:
(1)在图 2 中画出坐标系,并求抛物线的函数表达式.
(2)求 6 米材料恰好用完时$DE与CF$的长.
(3)种植区域分隔完成后,欣欣又想用灯带对该花坛进行装饰,计划将灯带围成一个矩形.她尝试借助图 2 设计矩形四个顶点的位置,其中两个顶点在抛物线上,另外两个顶点分别在线段$AC$,$BC$上.直接写出符合设计要求的矩形周长的最大值.
问题情境:如图 1,矩形$MNKL$是学校花园的示意图,其中一个花坛的轮廓可近似看成由抛物线的一部分与线段$AB$组成的封闭图形,点$A$,$B在矩形的边MN$上.现要对该花坛内种植区域进行划分,以种植不同花卉,学校面向全体同学征集设计方案.

方案设计:如图 2,$AB = 6$米,$AB的垂直平分线与抛物线交于点P$,与$AB交于点O$,点$P$是抛物线的顶点,且$PO = 9$米.欣欣设计的方案如下:
第一步:在线段$OP上确定点C$,使$∠ACB = 90^{\circ}$.用篱笆沿线段$AC$,$BC分隔出△ABC$区域,种植串串红;
第二步:在线段$CP上取点F$(不与$C$,$P$重合),过点$F作AB$的平行线,交抛物线于点$D$,$E$.用篱笆沿$DE$,$CF将线段AC$,$BC$与抛物线围成的区域分隔成三部分,分别种植不同花色的月季.

方案实施:学校采用了欣欣的方案,在完成第一步$△ABC$区域的分隔后,发现仅剩 6 米篱笆材料.若要在第二步分隔中恰好用完 6 米材料,需确定$DE与CF$的长.为此,欣欣在图 2 中以$AB所在直线为x$轴,$OP所在直线为y$轴建立平面直角坐标系.请按照她的方法解决问题:
(1)在图 2 中画出坐标系,并求抛物线的函数表达式.
(2)求 6 米材料恰好用完时$DE与CF$的长.
(3)种植区域分隔完成后,欣欣又想用灯带对该花坛进行装饰,计划将灯带围成一个矩形.她尝试借助图 2 设计矩形四个顶点的位置,其中两个顶点在抛物线上,另外两个顶点分别在线段$AC$,$BC$上.直接写出符合设计要求的矩形周长的最大值.
答案:
解析
(1) 建立如图所示的平面直角坐标系。

$\because OP$所在直线是$AB$的垂直平分线,且$AB = 6$,$\therefore OA = OB=\frac{1}{2}AB=\frac{1}{2}×6 = 3$。$\therefore$点$B$的坐标为$(3,0)$。$\because OP = 9$,$\therefore$点$P$的坐标为$(0,9)$。$\because$点$P$是抛物线的顶点,$\therefore$设抛物线的函数表达式为$y = ax^{2}+9$。$\because$点$B(3,0)$在抛物线$y = ax^{2}+9$上,$\therefore 9a + 9 = 0$,解得$a = -1$。$\therefore$抛物线的函数表达式为$y = -x^{2}+9(-3\leqslant x\leqslant 3)$。
(2) $\because$点$D$,$E$在抛物线$y = -x^{2}+9$上,$\therefore$设点$E$的坐标为$(m,-m^{2}+9)$。$\because DE// AB$,交$y$轴于点$F$,$\therefore DF = EF = m$,$OF = -m^{2}+9$。$\therefore DE = 2m$。$\because$在$Rt\triangle ABC$中,$∠ACB = 90^{\circ}$,$OA = OB$,$\therefore OC=\frac{1}{2}AB=\frac{1}{2}×6 = 3$。$\therefore CF = OF - OC = -m^{2}+9 - 3 = -m^{2}+6$。根据题意,得$DE + CF = 6$,$\therefore -m^{2}+6 + 2m = 6$。解得$m_{1}=2$,$m_{2}=0$(不符合题意,舍去),$\therefore m = 2$。$\therefore DE = 2m = 4$,$CF = -m^{2}+6 = 2$。
答:$DE$的长为$4$米,$CF$的长为$2$米。
(3) $\frac{33}{2}$。
详解:设矩形位于抛物线上的两个顶点分别为$J$,$I$,位于$AC$,$BC$上的两个顶点分别为$G$,$H$,如图。

设点$I$的横坐标为$n$,则点$I$的坐标为$(n,-n^{2}+9)$,点$J$的坐标为$(-n,-n^{2}+9)$,$\therefore JI = 2n$。
设$BC$所在直线的解析式为$y = kx + b$,易知$C(0,3)$,把$B(3,0)$,$C(0,3)$代入得$\left\{\begin{array}{l} 3k + b = 0,\\ b = 3,\end{array}\right.$解得$\left\{\begin{array}{l} k = -1,\\ b = 3,\end{array}\right.$ $\therefore y = -x + 3$,$\therefore$点$H$的坐标为$(n,-n + 3)$,
$\therefore IH = -n^{2}+9 - (-n + 3)= -n^{2}+n + 6$,
$\therefore$矩形$JIHG$的周长$= 2JI + 2IH = 4n + 2(-n^{2}+n + 6)= -2n^{2}+6n + 12 = -2(n - \frac{3}{2})^{2}+\frac{33}{2}$。
$\therefore$当$n=\frac{3}{2}$时,矩形$JIHG$的周长有最大值,最大值为$\frac{33}{2}$。
解析
(1) 建立如图所示的平面直角坐标系。

$\because OP$所在直线是$AB$的垂直平分线,且$AB = 6$,$\therefore OA = OB=\frac{1}{2}AB=\frac{1}{2}×6 = 3$。$\therefore$点$B$的坐标为$(3,0)$。$\because OP = 9$,$\therefore$点$P$的坐标为$(0,9)$。$\because$点$P$是抛物线的顶点,$\therefore$设抛物线的函数表达式为$y = ax^{2}+9$。$\because$点$B(3,0)$在抛物线$y = ax^{2}+9$上,$\therefore 9a + 9 = 0$,解得$a = -1$。$\therefore$抛物线的函数表达式为$y = -x^{2}+9(-3\leqslant x\leqslant 3)$。
(2) $\because$点$D$,$E$在抛物线$y = -x^{2}+9$上,$\therefore$设点$E$的坐标为$(m,-m^{2}+9)$。$\because DE// AB$,交$y$轴于点$F$,$\therefore DF = EF = m$,$OF = -m^{2}+9$。$\therefore DE = 2m$。$\because$在$Rt\triangle ABC$中,$∠ACB = 90^{\circ}$,$OA = OB$,$\therefore OC=\frac{1}{2}AB=\frac{1}{2}×6 = 3$。$\therefore CF = OF - OC = -m^{2}+9 - 3 = -m^{2}+6$。根据题意,得$DE + CF = 6$,$\therefore -m^{2}+6 + 2m = 6$。解得$m_{1}=2$,$m_{2}=0$(不符合题意,舍去),$\therefore m = 2$。$\therefore DE = 2m = 4$,$CF = -m^{2}+6 = 2$。
答:$DE$的长为$4$米,$CF$的长为$2$米。
(3) $\frac{33}{2}$。
详解:设矩形位于抛物线上的两个顶点分别为$J$,$I$,位于$AC$,$BC$上的两个顶点分别为$G$,$H$,如图。

设点$I$的横坐标为$n$,则点$I$的坐标为$(n,-n^{2}+9)$,点$J$的坐标为$(-n,-n^{2}+9)$,$\therefore JI = 2n$。
设$BC$所在直线的解析式为$y = kx + b$,易知$C(0,3)$,把$B(3,0)$,$C(0,3)$代入得$\left\{\begin{array}{l} 3k + b = 0,\\ b = 3,\end{array}\right.$解得$\left\{\begin{array}{l} k = -1,\\ b = 3,\end{array}\right.$ $\therefore y = -x + 3$,$\therefore$点$H$的坐标为$(n,-n + 3)$,
$\therefore IH = -n^{2}+9 - (-n + 3)= -n^{2}+n + 6$,
$\therefore$矩形$JIHG$的周长$= 2JI + 2IH = 4n + 2(-n^{2}+n + 6)= -2n^{2}+6n + 12 = -2(n - \frac{3}{2})^{2}+\frac{33}{2}$。
$\therefore$当$n=\frac{3}{2}$时,矩形$JIHG$的周长有最大值,最大值为$\frac{33}{2}$。