24.「2024 四川凉山州中考」(10 分)如图,抛物线 $ y = -x^2 + bx + c $ 与直线 $ y = x + 2 $ 相交于 $ A(-2,0),B(3,m) $ 两点,与 $ x $ 轴相交于另一点 $ C $.
(1)求抛物线的解析式.
(2)点 $ P $ 是直线 $ AB $ 上方抛物线上的一个动点(不与 $ A、B $ 重合),过点 $ P $ 作直线 $ PD \perp x $ 轴于点 $ D $,交直线 $ AB $ 于点 $ E $,当 $ PE = 2ED $ 时,求 $ P $ 点坐标.
(3)抛物线上是否存在点 $ M $ 使 $ \triangle ABM $ 的面积等于 $ \triangle ABC $ 面积的一半? 若存在,请直接写出点 $ M $ 的坐标;若不存在,请说明理由.
(1)求抛物线的解析式.
$y=-x^{2}+2x + 8$
(2)点 $ P $ 是直线 $ AB $ 上方抛物线上的一个动点(不与 $ A、B $ 重合),过点 $ P $ 作直线 $ PD \perp x $ 轴于点 $ D $,交直线 $ AB $ 于点 $ E $,当 $ PE = 2ED $ 时,求 $ P $ 点坐标.
$(1,9)$
(3)抛物线上是否存在点 $ M $ 使 $ \triangle ABM $ 的面积等于 $ \triangle ABC $ 面积的一半? 若存在,请直接写出点 $ M $ 的坐标;若不存在,请说明理由.
$(\frac {1+\sqrt {13}}{2},\frac {11+\sqrt {13}}{2})$或$(\frac {1-\sqrt {13}}{2},\frac {11-\sqrt {13}}{2})$或$(\frac {1+\sqrt {37}}{2},\frac {-1+\sqrt {37}}{2})$或$(\frac {1-\sqrt {37}}{2},\frac {-1-\sqrt {37}}{2})$
答案：24. 解析 (1)把$B(3,m)$代入$y=x + 2$得$m=3 + 2 = 5,\therefore B(3,5)$,把$A(-2,0),B(3,5)$代入$y=-x^{2}+bx+c$得$\left\{\begin{array}{l} -4 - 2b + c = 0\\ -9 + 3b + c = 5\end{array}\right. $,解得$\left\{\begin{array}{l} b = 2\\ c = 8\end{array}\right. $,$\therefore $抛物线的解析式为$y=-x^{2}+2x + 8$. ……… (3分)(2)设$P(t,-t^{2}+2t + 8)$,则$E(t,t + 2),D(t,0),\because PE=2ED,\therefore -t^{2}+2t + 8-(t + 2)=2(t + 2)$,解得$t = 1$或$t=-2$,当$t = 1$时,$-t^{2}+2t + 8 = 9$,满足题意;当$t=-2$时,$-t^{2}+2t + 8 = 0$,不满足题意.$\therefore P$点坐标为$(1,9)$. ……… (6分)(3)抛物线上存在点M,使$△ABM$的面积等于$△ABC$面积的一半,M的坐标为$(\frac {1+\sqrt {13}}{2},\frac {11+\sqrt {13}}{2})$或$(\frac {1-\sqrt {13}}{2},\frac {11-\sqrt {13}}{2})$或$(\frac {1+\sqrt {37}}{2},\frac {-1+\sqrt {37}}{2})$或$(\frac {1-\sqrt {37}}{2},\frac {-1-\sqrt {37}}{2})$. ………………… (10分)
25.「2025 广东江门开平期末」(10 分)
【知识技能】
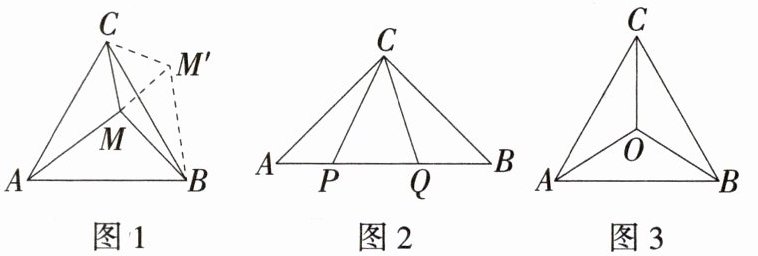
(1)如图 1,在等边三角形 $ ABC $ 内有一点 $ M $,若点 $ M $ 到顶点 $ C,A,B $ 的距离分别为 6,10,8,求 $ \angle BMC $ 的度数.
为了解决本题,我们可以将 $ \triangle AMC $ 绕顶点 $ C $ 逆时针旋转 $ 60^\circ $ 到 $ \triangle BM'C $ 处,此时 $ \triangle BM'C \cong \triangle AMC $,这样就可以利用旋转变换,将三条线段 $ AM,BM,CM $ 转化到一个三角形中,从而求得 $ \angle BMC = $____°.
【构建联系】
利用(1)的思想方法,解答下面的问题.
(2)如图 2,在 $ \triangle ABC $ 中,$ \angle ACB = 90^\circ,AC = BC,P,Q $ 为 $ AB $ 上的点,且 $ \angle PCQ = 45^\circ $,求证:$ PQ^2 = BQ^2 + AP^2 $.
【深入探究】
(3)如图 3,在等边三角形 $ ABC $ 中,$ AC = 2,O $ 为 $ \triangle ABC $ 内一点,连接 $ AO,BO,CO $,且 $ \angle AOC = \angle COB = \angle BOA = 120^\circ $,求 $ OA + OB + OC $ 的值.
【知识技能】
(1)如图 1,在等边三角形 $ ABC $ 内有一点 $ M $,若点 $ M $ 到顶点 $ C,A,B $ 的距离分别为 6,10,8,求 $ \angle BMC $ 的度数.
为了解决本题,我们可以将 $ \triangle AMC $ 绕顶点 $ C $ 逆时针旋转 $ 60^\circ $ 到 $ \triangle BM'C $ 处,此时 $ \triangle BM'C \cong \triangle AMC $,这样就可以利用旋转变换,将三条线段 $ AM,BM,CM $ 转化到一个三角形中,从而求得 $ \angle BMC = $____°.
【构建联系】
利用(1)的思想方法,解答下面的问题.
(2)如图 2,在 $ \triangle ABC $ 中,$ \angle ACB = 90^\circ,AC = BC,P,Q $ 为 $ AB $ 上的点,且 $ \angle PCQ = 45^\circ $,求证:$ PQ^2 = BQ^2 + AP^2 $.
【深入探究】
(3)如图 3,在等边三角形 $ ABC $ 中,$ AC = 2,O $ 为 $ \triangle ABC $ 内一点,连接 $ AO,BO,CO $,且 $ \angle AOC = \angle COB = \angle BOA = 120^\circ $,求 $ OA + OB + OC $ 的值.
答案：
25. 解析 (1)150. …………………………… (2分)(2)证明:如图,把$△ACP$绕点C逆时针旋转$90^{\circ }$得到$△BCP'$.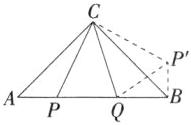
由旋转的性质得,$BP'=AP,CP'=CP,∠BCP'=∠ACP,∠CBP'=∠A,∠PCP'=90^{\circ },\because ∠PCQ=45^{\circ },\therefore ∠P'CQ=∠PCP'-∠PCQ=90^{\circ }-45^{\circ }=45^{\circ },\therefore ∠PCQ=∠P'CQ$,在$△PCQ$和$△P'CQ$中,$\left\{\begin{array}{l} CP = CP'\\ ∠PCQ=∠P'CQ\\ CQ = CQ\end{array}\right. $,$\therefore △PCQ\cong △P'CQ(SAS),\therefore PQ=P'Q$, …………………………… (4分)$\because ∠ACB=90^{\circ },AC=BC,\therefore ∠A=∠CBA=45^{\circ },\therefore ∠P'BQ=45^{\circ }+45^{\circ }=90^{\circ }$,在$Rt△P'BQ$中,由勾股定理得,$P'Q^{2}=BQ^{2}+BP'^{2}$,即$PQ^{2}=BQ^{2}+AP^{2}$. ……………………… (6分)(3)$\because △ABC$是等边三角形,$AC = 2,\therefore AB=BC=AC = 2,∠ABC=60^{\circ }$,如图,将$△AOC$绕点C逆时针旋转$60^{\circ }$到$△BO'C$处,连接$OO'$.
$\therefore CO=CO',AO=BO',∠OCO'=60^{\circ },∠CO'B=∠AOC=120^{\circ },\therefore △COO'$是等边三角形,$\therefore ∠COO'=∠CO'O=60^{\circ }.\because ∠AOC=∠COB=∠BOA=120^{\circ },\therefore ∠BOO'=∠BO'O=60^{\circ },\therefore △BOO'$是等边三角形,$∠AOB+∠BOO'=180^{\circ },\therefore A,O,O'$三点共线,$BO=BO'=CO'=OC,∠OBO'=60^{\circ },\therefore BC$垂直平分$OO',\therefore ∠CBO'=\frac {1}{2}∠OBO'=30^{\circ },\therefore ∠ABO'=90^{\circ },\therefore ∠BAO'=30^{\circ },\therefore AO'=2BO'$,在$Rt△ABO'$中,由勾股定理得$AB^{2}+BO'^{2}=AO'^{2},\therefore 2^{2}+BO'^{2}=4BO'^{2},\therefore BO'=\frac {2\sqrt {3}}{3}$,即$BO=\frac {2\sqrt {3}}{3},\therefore OA+OB+OC=2\sqrt {3}$. ………………… (10分)
25. 解析 (1)150. …………………………… (2分)(2)证明:如图,把$△ACP$绕点C逆时针旋转$90^{\circ }$得到$△BCP'$.
由旋转的性质得,$BP'=AP,CP'=CP,∠BCP'=∠ACP,∠CBP'=∠A,∠PCP'=90^{\circ },\because ∠PCQ=45^{\circ },\therefore ∠P'CQ=∠PCP'-∠PCQ=90^{\circ }-45^{\circ }=45^{\circ },\therefore ∠PCQ=∠P'CQ$,在$△PCQ$和$△P'CQ$中,$\left\{\begin{array}{l} CP = CP'\\ ∠PCQ=∠P'CQ\\ CQ = CQ\end{array}\right. $,$\therefore △PCQ\cong △P'CQ(SAS),\therefore PQ=P'Q$, …………………………… (4分)$\because ∠ACB=90^{\circ },AC=BC,\therefore ∠A=∠CBA=45^{\circ },\therefore ∠P'BQ=45^{\circ }+45^{\circ }=90^{\circ }$,在$Rt△P'BQ$中,由勾股定理得,$P'Q^{2}=BQ^{2}+BP'^{2}$,即$PQ^{2}=BQ^{2}+AP^{2}$. ……………………… (6分)(3)$\because △ABC$是等边三角形,$AC = 2,\therefore AB=BC=AC = 2,∠ABC=60^{\circ }$,如图,将$△AOC$绕点C逆时针旋转$60^{\circ }$到$△BO'C$处,连接$OO'$. $\therefore CO=CO',AO=BO',∠OCO'=60^{\circ },∠CO'B=∠AOC=120^{\circ },\therefore △COO'$是等边三角形,$\therefore ∠COO'=∠CO'O=60^{\circ }.\because ∠AOC=∠COB=∠BOA=120^{\circ },\therefore ∠BOO'=∠BO'O=60^{\circ },\therefore △BOO'$是等边三角形,$∠AOB+∠BOO'=180^{\circ },\therefore A,O,O'$三点共线,$BO=BO'=CO'=OC,∠OBO'=60^{\circ },\therefore BC$垂直平分$OO',\therefore ∠CBO'=\frac {1}{2}∠OBO'=30^{\circ },\therefore ∠ABO'=90^{\circ },\therefore ∠BAO'=30^{\circ },\therefore AO'=2BO'$,在$Rt△ABO'$中,由勾股定理得$AB^{2}+BO'^{2}=AO'^{2},\therefore 2^{2}+BO'^{2}=4BO'^{2},\therefore BO'=\frac {2\sqrt {3}}{3}$,即$BO=\frac {2\sqrt {3}}{3},\therefore OA+OB+OC=2\sqrt {3}$. ………………… (10分)