1.「2025广东广州天河月考」若$y= (m+1)x^{|m|+1}-(m-1)x+1$是关于x的二次函数,则m的值是 (
A. -1
B. 1
C. ±1
D. 0
B
)A. -1
B. 1
C. ±1
D. 0
答案:B ∵y=(m + 1)x|m| + 1−(m - 1)x + 1是关于x的二次函数,∴|m| + 1 = 2且m + 1≠0,解得m = 1。故选B。
2.「2025山东德州齐河月考」若函数$y= (m^{2}+m)x^{m^{2}-2m-1}$是关于x的二次函数,则m的值是
3
.答案:答案3
解析 由y=(m² + m)xm²−2m−1是关于x的二次函数,得m²−2m−1 = 2且m² + m≠0,解得m = 3。
解析 由y=(m² + m)xm²−2m−1是关于x的二次函数,得m²−2m−1 = 2且m² + m≠0,解得m = 3。
3.「2025湖南湘西州凤凰月考」若二次函数$y= (m+3)x^{2}-5x+(m^{2}-9)$的图象经过原点,则$m=$
3
.答案:答案3
解析 ∵二次函数y=(m + 3)x²−5x + (m²−9)的图象经过原点,∴m + 3≠0且m²−9 = 0,解得m = 3。
解析 ∵二次函数y=(m + 3)x²−5x + (m²−9)的图象经过原点,∴m + 3≠0且m²−9 = 0,解得m = 3。
4.「2024浙江温州鹿城三模」已知二次函数$y= a(x-1)^{2}-a(a≠0)$,当$-1≤x≤4$时,y的最小值为-4,则a的值为 (
A. $\frac {1}{2}$或4
B. 4或$-\frac {1}{2}$
C. $-\frac {4}{3}$或4
D. $-\frac {1}{2}或\frac {4}{3}$
B
)A. $\frac {1}{2}$或4
B. 4或$-\frac {1}{2}$
C. $-\frac {4}{3}$或4
D. $-\frac {1}{2}或\frac {4}{3}$
答案:B 抛物线y=a(x - 1)² - a的对称轴为直线x = 1,顶点坐标为(1, - a),若a>0,则在 - 1≤x≤4的范围内,函数有最小值,为 - a,∵y的最小值为 - 4,∴ - a = - 4,∴a = 4;若a<0,则在 - 1≤x≤4的范围内,当x = 4时,函数有最小值,∴9a - a = - 4,解得a = - $\frac{1}{2}$。综上所述,a的值为4或 - $\frac{1}{2}$。故选B。
5.「2025江西宜春高安期中」如果抛物线$y= -x^{2}+3x-2$沿x轴向左平移m个单位长度后经过原点,那么$m=$
1或2
.答案:答案 1或2
解析 y = - x² + 3x - 2 = - (x - $\frac{3}{2}$)² + $\frac{1}{4}$,∴抛物线沿x轴向左平移m个单位长度,平移后抛物线的解析式为y = - (x - $\frac{3}{2}$ + m)² + $\frac{1}{4}$,把(0,0)代入可得 - (m - $\frac{3}{2}$)² + $\frac{1}{4}$ = 0,解得m₁ = 1,m₂ = 2。
解析 y = - x² + 3x - 2 = - (x - $\frac{3}{2}$)² + $\frac{1}{4}$,∴抛物线沿x轴向左平移m个单位长度,平移后抛物线的解析式为y = - (x - $\frac{3}{2}$ + m)² + $\frac{1}{4}$,把(0,0)代入可得 - (m - $\frac{3}{2}$)² + $\frac{1}{4}$ = 0,解得m₁ = 1,m₂ = 2。
6.「2024广西柳州期末」已知二次函数$y= 3(x-a)^{2}$的图象上,当$x>2$时,y随x的增大而增大,则a的取值范围是
a≤2
.答案:答案 a≤2
解析 二次函数y = 3(x - a)²的对称轴为直线x = a,图象开口向上,∵当x>a时,y的值随x值的增大而增大,∴a≤2。
解析 二次函数y = 3(x - a)²的对称轴为直线x = a,图象开口向上,∵当x>a时,y的值随x值的增大而增大,∴a≤2。
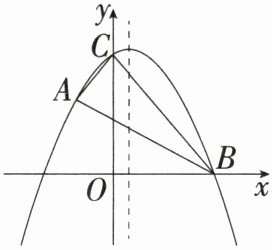
7.「2024安徽淮南大通月考」如图,在平面直角坐标系中,抛物线$y= -\frac {1}{2}x^{2}+\frac {1}{2}x+3$与x轴正半轴交于点B,与y轴交于点C,且过点$A(-1,2)$,连接AB,AC,BC.
(1)求$\triangle ABC$的面积.
(2)若点P是抛物线对称轴上一点,且$S_{\triangle ABC}= 2S_{\triangle BCP}$,求点P的坐标.
(1)求$\triangle ABC$的面积.
(2)若点P是抛物线对称轴上一点,且$S_{\triangle ABC}= 2S_{\triangle BCP}$,求点P的坐标.

答案:
解析 (1)把y = 0代入y = - $\frac{1}{2}$x² + $\frac{1}{2}$x + 3,得 - $\frac{1}{2}$x² + $\frac{1}{2}$x + 3 = 0,解得x₁ = - 2,x₂ = 3,∴B(3,0)。
把x = 0代入y = - $\frac{1}{2}$x² + $\frac{1}{2}$x + 3,得y = 3,∴C(0,3)。
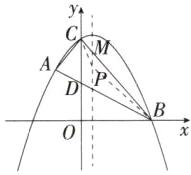
设直线AB的解析式为y = kx + b(k≠0),直线AB与y轴相交于点D,如图。
把A( - 1,2)、B(3,0)代入y = kx + b,得$\begin{cases}2 = - k + b\\0 = 3k + b\end{cases}$,
解得$\begin{cases}k = - \frac{1}{2}\\b = \frac{3}{2}\end{cases}$,∴直线AB的解析式为y = - $\frac{1}{2}$x + $\frac{3}{2}$。
当x = 0时,y = $\frac{3}{2}$,∴D(0,$\frac{3}{2}$),∴CD = 3 - $\frac{3}{2}$ = $\frac{3}{2}$。
∴S△ABC = S△ACD + S△BCD = $\frac{1}{2}$×$\frac{3}{2}$×1 + $\frac{1}{2}$×$\frac{3}{2}$×3 = 3。

(2)由y = - $\frac{1}{2}$x² + $\frac{1}{2}$x + 3可得抛物线的对称轴为直线x = $\frac{1}{2}$,设直线BC的解析式为y = mx + n(m≠0)。
把B(3,0),C(0,3)代入,得$\begin{cases}0 = 3m + n\\3 = n\end{cases}$,解得$\begin{cases}m = - 1\\n = 3\end{cases}$,∴直线BC的解析式为y = - x + 3。
如图,设直线BC与抛物线对称轴相交于点M,点P的坐标为($\frac{1}{2}$,p),把x = $\frac{1}{2}$代入y = - x + 3,得y = - $\frac{1}{2}$ + 3 = $\frac{5}{2}$,∴M($\frac{1}{2}$,$\frac{5}{2}$),∴PM = |$\frac{5}{2}$ - p|。
∴S△BCP = S△CPM + S△BPM = $\frac{1}{2}$×$\frac{1}{2}$×|$\frac{5}{2}$ - p| + $\frac{1}{2}$×(3 - $\frac{1}{2}$)×|$\frac{5}{2}$ - p| = $\frac{3}{2}$×|$\frac{5}{2}$ - p|,∵S△ABC = 2S△BCP,∴2S△BCP = 3,
∴2×$\frac{3}{2}$×|$\frac{5}{2}$ - p| = 3,即|$\frac{5}{2}$ - p| = 1,解得p = $\frac{3}{2}$或p = $\frac{7}{2}$,∴点P的坐标为($\frac{1}{2}$,$\frac{3}{2}$)或($\frac{1}{2}$,$\frac{7}{2}$)。
解析 (1)把y = 0代入y = - $\frac{1}{2}$x² + $\frac{1}{2}$x + 3,得 - $\frac{1}{2}$x² + $\frac{1}{2}$x + 3 = 0,解得x₁ = - 2,x₂ = 3,∴B(3,0)。
把x = 0代入y = - $\frac{1}{2}$x² + $\frac{1}{2}$x + 3,得y = 3,∴C(0,3)。
设直线AB的解析式为y = kx + b(k≠0),直线AB与y轴相交于点D,如图。
把A( - 1,2)、B(3,0)代入y = kx + b,得$\begin{cases}2 = - k + b\\0 = 3k + b\end{cases}$,
解得$\begin{cases}k = - \frac{1}{2}\\b = \frac{3}{2}\end{cases}$,∴直线AB的解析式为y = - $\frac{1}{2}$x + $\frac{3}{2}$。
当x = 0时,y = $\frac{3}{2}$,∴D(0,$\frac{3}{2}$),∴CD = 3 - $\frac{3}{2}$ = $\frac{3}{2}$。
∴S△ABC = S△ACD + S△BCD = $\frac{1}{2}$×$\frac{3}{2}$×1 + $\frac{1}{2}$×$\frac{3}{2}$×3 = 3。

(2)由y = - $\frac{1}{2}$x² + $\frac{1}{2}$x + 3可得抛物线的对称轴为直线x = $\frac{1}{2}$,设直线BC的解析式为y = mx + n(m≠0)。
把B(3,0),C(0,3)代入,得$\begin{cases}0 = 3m + n\\3 = n\end{cases}$,解得$\begin{cases}m = - 1\\n = 3\end{cases}$,∴直线BC的解析式为y = - x + 3。
如图,设直线BC与抛物线对称轴相交于点M,点P的坐标为($\frac{1}{2}$,p),把x = $\frac{1}{2}$代入y = - x + 3,得y = - $\frac{1}{2}$ + 3 = $\frac{5}{2}$,∴M($\frac{1}{2}$,$\frac{5}{2}$),∴PM = |$\frac{5}{2}$ - p|。
∴S△BCP = S△CPM + S△BPM = $\frac{1}{2}$×$\frac{1}{2}$×|$\frac{5}{2}$ - p| + $\frac{1}{2}$×(3 - $\frac{1}{2}$)×|$\frac{5}{2}$ - p| = $\frac{3}{2}$×|$\frac{5}{2}$ - p|,∵S△ABC = 2S△BCP,∴2S△BCP = 3,
∴2×$\frac{3}{2}$×|$\frac{5}{2}$ - p| = 3,即|$\frac{5}{2}$ - p| = 1,解得p = $\frac{3}{2}$或p = $\frac{7}{2}$,∴点P的坐标为($\frac{1}{2}$,$\frac{3}{2}$)或($\frac{1}{2}$,$\frac{7}{2}$)。

8.「2025安徽蚌埠蚌山月考」函数$y= -\frac {1}{2}x^{2}-x(-2≤x≤2)$的最大值和最小值分别为 (
A. $\frac {1}{2}$和-4
B. 0和-4
C. $\frac {1}{2}$和0
D. $\frac {1}{2}$和-6
A
)A. $\frac {1}{2}$和-4
B. 0和-4
C. $\frac {1}{2}$和0
D. $\frac {1}{2}$和-6
答案:A 由题意知,y = - $\frac{1}{2}$x² - x = - $\frac{1}{2}$(x + 1)² + $\frac{1}{2}$,∴对称轴为直线x = - 1,∵a = - $\frac{1}{2}$<0,∴当x = - 1时,y有最大值,为$\frac{1}{2}$;当x = - 2时,y = 0;当x = 2时,y = - 4,∵ - 4<0,∴y的最小值为 - 4。∴函数y = - $\frac{1}{2}$x² - x( - 2≤x≤2)的最大值和最小值分别为$\frac{1}{2}$和 - 4。故选A。
9.「2025甘肃武威凉州期中」已知二次函数$y= -2(x+1)^{2}+3$,当$-2<x<3$时,函数值y的取值范围是
-29<y≤3
.答案:答案 - 29<y≤3
解析 由题可知函数图象的顶点坐标为( - 1,3),对称轴为直线x = - 1,图象开口向下,∴当x = - 1时,函数有最大值,为3。∵ - 2<x<3,∴当x = - 2时,函数值y = 1,当x = 3时,函数值y = - 29,∴当 - 2<x<3时,函数值y的取值范围是 - 29<y≤3。
解析 由题可知函数图象的顶点坐标为( - 1,3),对称轴为直线x = - 1,图象开口向下,∴当x = - 1时,函数有最大值,为3。∵ - 2<x<3,∴当x = - 2时,函数值y = 1,当x = 3时,函数值y = - 29,∴当 - 2<x<3时,函数值y的取值范围是 - 29<y≤3。
10.「2025浙江温州瑞安月考」已知$2x-y= 8$,若$-1≤x≤3$,则xy的最大值为
10
.答案:答案 10
解析 ∵2x - y = 8,∴y = 2x - 8,∴xy = x(2x - 8) = 2x² - 8x = 2(x² - 4x) = 2(x - 2)² - 8,设z = 2(x - 2)² - 8,易知抛物线z = 2(x - 2)² - 8的开口向上,对称轴为直线x = 2,∵| - 1 - 2|>|3 - 2|,∴当x = - 1时,xy有最大值,为2×9 - 8 = 10。
解析 ∵2x - y = 8,∴y = 2x - 8,∴xy = x(2x - 8) = 2x² - 8x = 2(x² - 4x) = 2(x - 2)² - 8,设z = 2(x - 2)² - 8,易知抛物线z = 2(x - 2)² - 8的开口向上,对称轴为直线x = 2,∵| - 1 - 2|>|3 - 2|,∴当x = - 1时,xy有最大值,为2×9 - 8 = 10。
11.「2025浙江杭州拱墅月考」已知函数$y= x^{2}+bx+c$(b,c为常数)的图象经过点$(0,3),(6,3)$.
(1)求b,c的值.
(2)当$0≤x≤4$时,求y的最大值与最小值之差.
(3)当$-2≤x≤k$时,求y的最小值.(可用含k的代数式表示)
(1)求b,c的值.
(2)当$0≤x≤4$时,求y的最大值与最小值之差.
(3)当$-2≤x≤k$时,求y的最小值.(可用含k的代数式表示)
答案:解析 (1)∵函数y = x² + bx + c(b,c为常数)的图象经过点(0,3),(6,3),
∴$\begin{cases}c = 3\\36 + 6b + c = 3\end{cases}$,解得$\begin{cases}b = - 6\\c = 3\end{cases}$。
(2)由(1)得,y = x² - 6x + 3 = (x - 3)² - 6。
∵0≤x≤4,
∴当x = 3时,y取得最小值,此时y = - 6。
当x = 0时,y取得最大值,此时y = (0 - 3)² - 6 = 3。
∵3 - ( - 6) = 9,∴当0≤x≤4时,y的最大值与最小值之差为9。
(3)y = x² - 6x + 3 = (x - 3)² - 6。
若 - 2<k≤3,则 - 2≤x≤k时,y随x的增大而减小,
∴当x = k时,y有最小值,为y = k² - 6k + 3;
若k>3,则 - 2≤x≤k时,抛物线的顶点为图象最低点,∴当x = 3时,y有最小值,为 - 6。
综上所述,y的最小值为k² - 6k + 3或 - 6。
∴$\begin{cases}c = 3\\36 + 6b + c = 3\end{cases}$,解得$\begin{cases}b = - 6\\c = 3\end{cases}$。
(2)由(1)得,y = x² - 6x + 3 = (x - 3)² - 6。
∵0≤x≤4,
∴当x = 3时,y取得最小值,此时y = - 6。
当x = 0时,y取得最大值,此时y = (0 - 3)² - 6 = 3。
∵3 - ( - 6) = 9,∴当0≤x≤4时,y的最大值与最小值之差为9。
(3)y = x² - 6x + 3 = (x - 3)² - 6。
若 - 2<k≤3,则 - 2≤x≤k时,y随x的增大而减小,
∴当x = k时,y有最小值,为y = k² - 6k + 3;
若k>3,则 - 2≤x≤k时,抛物线的顶点为图象最低点,∴当x = 3时,y有最小值,为 - 6。
综上所述,y的最小值为k² - 6k + 3或 - 6。