12. [2022黑龙江大庆中考]已知函数$y= mx^{2}+3mx+m-1$的图象与坐标轴恰有两个公共点,则实数m的值为
1或 - $\frac{4}{5}$
.答案:答案1或 - $\frac{4}{5}$
解析 当m = 0时,y = - 1,图象与坐标轴只有一个公共点,不符合题意。当m ≠ 0时,∵函数y = mx² + 3mx + m - 1的图象与坐标轴恰有两个公共点,∴①过坐标原点,m - 1 = 0,∴m = 1(经检验满足题意),②与x轴、y轴各有一个公共点,Δ = 0,即(3m)² - 4m(m - 1) = 0,解得m = 0(舍去)或m = - $\frac{4}{5}$(经检验满足题意)。综上所述,m的值为1或 - $\frac{4}{5}$。
解析 当m = 0时,y = - 1,图象与坐标轴只有一个公共点,不符合题意。当m ≠ 0时,∵函数y = mx² + 3mx + m - 1的图象与坐标轴恰有两个公共点,∴①过坐标原点,m - 1 = 0,∴m = 1(经检验满足题意),②与x轴、y轴各有一个公共点,Δ = 0,即(3m)² - 4m(m - 1) = 0,解得m = 0(舍去)或m = - $\frac{4}{5}$(经检验满足题意)。综上所述,m的值为1或 - $\frac{4}{5}$。
13. [2025北京海淀期中]如图,在平面直角坐标系xOy中,抛物线$y= 3x^{2}+bx+c$与x轴交于A,B两点,且$AB= 4$.若将此抛物线先向左平移2个单位,再向下平移m个单位,所得新抛物线与x轴的两个交点间的距离为8,则m的值为(
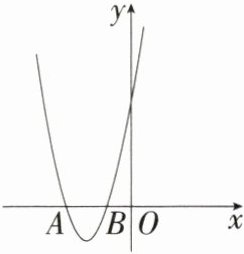
A. 6
B. 2
C. 24
D. 36
D
)
A. 6
B. 2
C. 24
D. 36
答案:D 当y = 0时,设3x² + bx + c = 0的两根为x₁、x₂,则x₁ + x₂ = - $\frac{b}{3}$,x₁·x₂ = $\frac{c}{3}$,∵AB = 4,∴|x₁ - x₂| = 4,∴(x₁ - x₂)² = (x₁ + x₂)² - 4x₁x₂ = 16,∴b² - 12c = 144,∵抛物线平移后所得新抛物线与x轴的两个交点间的距离为8,即当y = m时,抛物线上两点之间的距离为8。设3x² + bx + c = m的两根为x₃、x₄,则x₃ + x₄ = - $\frac{b}{3}$,x₃·x₄ = $\frac{c - m}{3}$,|x₃ - x₄| = 8,∴(x₃ - x₄)² = (x₃ + x₄)² - 4x₃x₄ = 64,∴b² - 12(c - m) = b² - 12c + 12m = 576,∵b² - 12c = 144,∴144 + 12m = 576,解得m = 36。故选D。
14. 如图,已知抛物线$y= ax^{2}+bx+c(a,b,c$为常数,$a≠0)$交x轴于$A(1,0)$、$B(3,0)$两点,交y轴于$C(0,3)$,将该抛物线位于直线$y= m$(m为常数,$m≥0$)下方的部分沿直线$y= m$翻折,其余部分不变,得到的新图象记为“图象W”.
(1)求翻折前抛物线的表达式.
(2)若$m= 0$,直线$y= x+n$与图象W有三个交点,求n的值.
(1)翻折前抛物线的表达式为$y=$
(2)n的值是
(1)求翻折前抛物线的表达式.
(2)若$m= 0$,直线$y= x+n$与图象W有三个交点,求n的值.
(1)翻折前抛物线的表达式为$y=$
$x² - 4x + 3$
。(2)n的值是
$-1$
或$-\frac{3}{4}$
。答案:解析 (1)由题意得$\begin{cases}a + b + c = 0 \\9a + 3b + c = 0 \\c = 3\end{cases}$,解得$\begin{cases}a = 1 \\b = - 4 \\c = 3\end{cases}$
∴翻折前抛物线的表达式为y = x² - 4x + 3。
(2)当m = 0,且直线y = x + n与图象W有三个交点时,存在两种情况:
①当直线y = x + n过点A时,与图象W有三个交点,此时n = - 1;
②当直线y = x + n与图象W位于线段AB正上方的部分仅有一个交点时,x + n = - x² + 4x - 3,即x² - 3x + n + 3 = 0,则Δ = ( - 3)² - 4×1×(n + 3) = 0,∴n = - $\frac{3}{4}$。
综上,n的值是 - 1或 - $\frac{3}{4}$。
∴翻折前抛物线的表达式为y = x² - 4x + 3。
(2)当m = 0,且直线y = x + n与图象W有三个交点时,存在两种情况:
①当直线y = x + n过点A时,与图象W有三个交点,此时n = - 1;
②当直线y = x + n与图象W位于线段AB正上方的部分仅有一个交点时,x + n = - x² + 4x - 3,即x² - 3x + n + 3 = 0,则Δ = ( - 3)² - 4×1×(n + 3) = 0,∴n = - $\frac{3}{4}$。
综上,n的值是 - 1或 - $\frac{3}{4}$。
1. [2025江苏盐城期中]已知点$(-2,5),(4,5)$是抛物线上的两点,则此抛物线的对称轴为____
直线x = 1
.答案:答案直线x = 1
解析 ∵点( - 2,5),(4,5)的纵坐标相同,∴两点关于抛物线的对称轴对称,∴抛物线的对称轴为直线x = $\frac{- 2 + 4}{2}$ = 1。
解析 ∵点( - 2,5),(4,5)的纵坐标相同,∴两点关于抛物线的对称轴对称,∴抛物线的对称轴为直线x = $\frac{- 2 + 4}{2}$ = 1。
2. [2025山东滨州滨城期中]已知二次函数$y= 2025x^{2}+k的图象上有两个不同点M(t_{1},4),N(t_{2},4)$,则$2025t_{1}+2025t_{2}= $
0
.答案:答案0
解析 ∵y = 2025x² + k,∴抛物线的对称轴为y轴,∵M(t₁,4),N(t₂,4)的纵坐标相等,∴点M、N关于y轴对称,∴t₁ + t₂ = 0,∴2025t₁ + 2025t₂ = 2025(t₁ + t₂) = 0。
解析 ∵y = 2025x² + k,∴抛物线的对称轴为y轴,∵M(t₁,4),N(t₂,4)的纵坐标相等,∴点M、N关于y轴对称,∴t₁ + t₂ = 0,∴2025t₁ + 2025t₂ = 2025(t₁ + t₂) = 0。
3. [2025浙江金华义乌月考改编]已知二次函数$y= x^{2}+bx+c$中,函数y与自变量x的部分对应值如表:

若$A(m,y_{1}),B(m+2,y_{2})$两点都在该函数的图象上,则当$m= $

若$A(m,y_{1}),B(m+2,y_{2})$两点都在该函数的图象上,则当$m= $
1
时,$y_{1}= y_{2}$.答案:答案1
解析 ∵x = 0时,y = 5;x = 4时,y = 5,∴该抛物线的对称轴为直线x = 2,∵A(m,y₁),B(m + 2,y₂)两点都在该函数的图象上,且y₁ = y₂,∴$\frac{m + m + 2}{2}$ = 2,解得m = 1。
解析 ∵x = 0时,y = 5;x = 4时,y = 5,∴该抛物线的对称轴为直线x = 2,∵A(m,y₁),B(m + 2,y₂)两点都在该函数的图象上,且y₁ = y₂,∴$\frac{m + m + 2}{2}$ = 2,解得m = 1。
4. [2023山东青岛十三中一模]已知二次函数$y= a(x-2)^{2}-3$的部分图象如图所示,若$y≤0$,则x的取值范围为

-1 ≤ x ≤ 5
.
答案:答案 - 1 ≤ x ≤ 5
解析 ∵y = a(x - 2)² - 3,∴抛物线的对称轴为直线x = 2,∵抛物线与x轴的一个交点为( - 1,0),( - 1,0)关于直线x = 2对称的点为(5,0),∴抛物线与x轴的另一个交点为(5,0),∴y ≤ 0时,x的取值范围是 - 1 ≤ x ≤ 5。故答案为 - 1 ≤ x ≤ 5。
解析 ∵y = a(x - 2)² - 3,∴抛物线的对称轴为直线x = 2,∵抛物线与x轴的一个交点为( - 1,0),( - 1,0)关于直线x = 2对称的点为(5,0),∴抛物线与x轴的另一个交点为(5,0),∴y ≤ 0时,x的取值范围是 - 1 ≤ x ≤ 5。故答案为 - 1 ≤ x ≤ 5。