6. [2024天津和平月考]如图,要围一个矩形菜园ABCD,其中一边AD靠墙,且AD的长不能超过26m,其余的三边AB,BC,CD用篱笆围成,且这三边的和为40m,有下列结论:
①AB的长可以为6m;
②AB的长有两个不同的值满足菜园ABCD的面积为$192m^2$的条件;
③菜园ABCD面积的最大值为$210m^2.$
其中,正确结论的个数是(

A.0
B.1
C.2
D.3
①AB的长可以为6m;
②AB的长有两个不同的值满足菜园ABCD的面积为$192m^2$的条件;
③菜园ABCD面积的最大值为$210m^2.$
其中,正确结论的个数是(
B
)
A.0
B.1
C.2
D.3
答案:6.B 设AD的长为x m,则AB的长为$\frac{40 - x}{2}m$,当AB = 6m时,$\frac{40 - x}{2}=6$,解得x = 28,∵AD的长不能超过26m,∴x≤26,故①错误.∵菜园ABCD的面积为192m²,∴$x\cdot\frac{40 - x}{2}=192$,整理,得x² - 40x + 384 = 0,解得x = 24或x = 16,∴AB的长有两个不同的值满足菜园ABCD的面积为192m²的条件,故②正确.设矩形菜园的面积为y m²,根据题意,得$y=x\cdot\frac{40 - x}{2}=-\frac{1}{2}(x^{2}-40x)=-\frac{1}{2}(x - 20)^{2}+200$,∵$-\frac{1}{2}<0$,20 < 26,∴当x = 20时,y有最大值,为200,故③错误.故正确的结论有1个.故选B.
7. [2025安徽亳州利辛期中]九年级2班计划在劳动实践基地内种植蔬菜,班长买回来8米长的围栏,准备围成一边靠墙(墙足够长)的菜园,为了让菜园面积尽可能大,同学们提出了围成矩形、等腰三角形(底边靠墙)、半圆形这三种方案,如图,最佳方案是( )

A.方案1
B.方案2
C.方案3
D.三个方案都是最佳方案

A.方案1
B.方案2
C.方案3
D.三个方案都是最佳方案
答案:
7.C 方案1:设矩形的面积为S平方米,垂直于墙的一边长为x米,则平行于墙的一边长为(8 - 2x)米,则S = x(8 - 2x)=-2(x - 2)² + 8,∴当x = 2时,菜园面积有最大值,为8平方米;
方案2:如图,设等腰三角形为△ABC,其中AB = AC = 4米,作BH⊥AC交AC于H,由题意可得BH≤AB,即BH≤4米,∵△ABC的面积$=\frac{1}{2}AC\cdot BH$,∴当BH = 4米时,菜园面积有最大值,为$\frac{1}{2}\times4\times4 = 8$(平方米);

方案3:半圆的半径为$\frac{8}{\pi}$米,此时菜园的面积为$\frac{1}{2}\pi\times(\frac{8}{\pi})^{2}=\frac{32}{\pi}$(平方米).∵$\frac{32}{\pi}>8$,∴方案3是最佳方案.故选C.
7.C 方案1:设矩形的面积为S平方米,垂直于墙的一边长为x米,则平行于墙的一边长为(8 - 2x)米,则S = x(8 - 2x)=-2(x - 2)² + 8,∴当x = 2时,菜园面积有最大值,为8平方米;
方案2:如图,设等腰三角形为△ABC,其中AB = AC = 4米,作BH⊥AC交AC于H,由题意可得BH≤AB,即BH≤4米,∵△ABC的面积$=\frac{1}{2}AC\cdot BH$,∴当BH = 4米时,菜园面积有最大值,为$\frac{1}{2}\times4\times4 = 8$(平方米);

方案3:半圆的半径为$\frac{8}{\pi}$米,此时菜园的面积为$\frac{1}{2}\pi\times(\frac{8}{\pi})^{2}=\frac{32}{\pi}$(平方米).∵$\frac{32}{\pi}>8$,∴方案3是最佳方案.故选C.
8. [2024广东韶关仁化期末]某校计划利用一片空地建一个学生自行车车棚,其中一面靠墙,墙的最大可用长度为12米.其余三边用总长为26米的木板材料围成.车棚形状如图1(矩形ABCD).为了方便学生出行,学校决定在与墙平行的一边开一个2米宽的门.
(1)求这个车棚的最大面积,此时AB与AD的长分别为多少米.
最大面积为
(2)如图2,在(1)的结论下,为了方便学生取车,施工单位决定在车棚内修建几条等宽的小路,使得停放自行车的面积为70平方米,那么小路的宽度是多少米?
小路的宽度是
(1)求这个车棚的最大面积,此时AB与AD的长分别为多少米.
最大面积为
96
平方米,此时AB为8
米,AD为12
米.(2)如图2,在(1)的结论下,为了方便学生取车,施工单位决定在车棚内修建几条等宽的小路,使得停放自行车的面积为70平方米,那么小路的宽度是多少米?
小路的宽度是
1
米.答案:8.解析 (1)设车棚的面积为S平方米,垂直于墙的边AB = x米,则平行于墙的边BC = (26 - 2x + 2)米,则S = x(28 - 2x)=-2x² + 28x=-2(x - 7)² + 98,由题意得26 - 2x + 2≤12,26 - 2x>0,∴8≤x<13,∴当x = 8时,S有最大值,此时AB = 8米,AD = 12米,面积为96平方米.
(2)设小路的宽度为a米,由(1)知车棚的最大面积为96平方米,AB = 8米,AD = 12米,当停放自行车的面积为70平方米时,小路的占地面积为96 - 70 = 26(平方米),∴2×8a + 12a - 2a² = 26,解得a = 1或a = 13(不合题意,舍去).
答:小路的宽度为1米.
(2)设小路的宽度为a米,由(1)知车棚的最大面积为96平方米,AB = 8米,AD = 12米,当停放自行车的面积为70平方米时,小路的占地面积为96 - 70 = 26(平方米),∴2×8a + 12a - 2a² = 26,解得a = 1或a = 13(不合题意,舍去).
答:小路的宽度为1米.
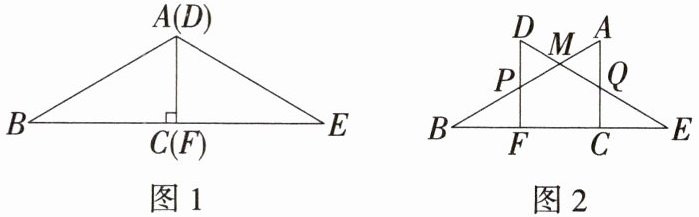
9. 如图1,放置两个全等的含有30°角的直角三角尺ABC与DEF(∠B= ∠E= 30°).若将三角尺ABC向右以每秒1个单位长度的速度移动(点C与点E重合时移动终止),移动过程中始终保持点B,F,C,E在同一条直线上,如图2,AB与DF,DE分别交于点P,M,AC与DE交于点Q,其中AC= DF= √3,设三角尺ABC的移动时间为x秒.
(1)在移动过程中,试用含x的代数式表示△AMQ的面积.
(2)当x等于多少时,两个三角尺重叠部分的面积有最大值?最大值是多少?
(1)在移动过程中,试用含x的代数式表示△AMQ的面积.
(2)当x等于多少时,两个三角尺重叠部分的面积有最大值?最大值是多少?

答案:
9.解析 (1)∵在Rt△ABC中,∠B = 30°,∴∠A = 60°.
∵∠E = 30°,∴∠EQC = ∠AQM = 60°,
∴△AMQ为等边三角形,
如图,过点M作MN⊥AQ,垂足为N.
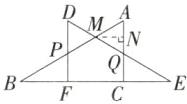
在Rt△ABC中,∠B = 30°,AC = $\sqrt{3}$,则BC = 3,
∴EF = BC = 3.根据题意知CF = x,
∴CE = EF - CF = 3 - x,易得$CQ=\frac{\sqrt{3}}{3}(3 - x)$,
∴$AQ=AC - CQ=\sqrt{3}-\frac{\sqrt{3}}{3}(3 - x)=\frac{\sqrt{3}}{3}x$,
∴$AM=AQ=\frac{\sqrt{3}}{3}x$,∴$MN=\frac{1}{2}x$,
∴$S_{\triangle AMQ}=\frac{1}{2}AQ\cdot MN=\frac{1}{2}\times\frac{\sqrt{3}}{3}x\cdot\frac{1}{2}x=\frac{\sqrt{3}}{12}x^{2}$.
(2)由(1)知BF = CE = 3 - x,$PF=\frac{\sqrt{3}}{3}(3 - x)$,
设两个三角尺重叠部分的面积为$S_{重叠}$,
∴$S_{重叠}=S_{\triangle ABC}-S_{\triangle AMQ}-S_{\triangle BPF}=\frac{1}{2}AC\cdot BC - S_{\triangle AMQ}-\frac{1}{2}BF\cdot PF=\frac{1}{2}\times\sqrt{3}\times3-\frac{\sqrt{3}}{12}x^{2}-\frac{1}{2}(3 - x)\cdot\frac{\sqrt{3}}{3}(3 - x)=-\frac{\sqrt{3}}{4}x^{2}+\sqrt{3}x=-\frac{\sqrt{3}}{4}(x - 2)^{2}+\sqrt{3}$,
∴当x = 2时,重叠部分面积有最大值,最大值是$\sqrt{3}$.
9.解析 (1)∵在Rt△ABC中,∠B = 30°,∴∠A = 60°.
∵∠E = 30°,∴∠EQC = ∠AQM = 60°,
∴△AMQ为等边三角形,
如图,过点M作MN⊥AQ,垂足为N.

在Rt△ABC中,∠B = 30°,AC = $\sqrt{3}$,则BC = 3,
∴EF = BC = 3.根据题意知CF = x,
∴CE = EF - CF = 3 - x,易得$CQ=\frac{\sqrt{3}}{3}(3 - x)$,
∴$AQ=AC - CQ=\sqrt{3}-\frac{\sqrt{3}}{3}(3 - x)=\frac{\sqrt{3}}{3}x$,
∴$AM=AQ=\frac{\sqrt{3}}{3}x$,∴$MN=\frac{1}{2}x$,
∴$S_{\triangle AMQ}=\frac{1}{2}AQ\cdot MN=\frac{1}{2}\times\frac{\sqrt{3}}{3}x\cdot\frac{1}{2}x=\frac{\sqrt{3}}{12}x^{2}$.
(2)由(1)知BF = CE = 3 - x,$PF=\frac{\sqrt{3}}{3}(3 - x)$,
设两个三角尺重叠部分的面积为$S_{重叠}$,
∴$S_{重叠}=S_{\triangle ABC}-S_{\triangle AMQ}-S_{\triangle BPF}=\frac{1}{2}AC\cdot BC - S_{\triangle AMQ}-\frac{1}{2}BF\cdot PF=\frac{1}{2}\times\sqrt{3}\times3-\frac{\sqrt{3}}{12}x^{2}-\frac{1}{2}(3 - x)\cdot\frac{\sqrt{3}}{3}(3 - x)=-\frac{\sqrt{3}}{4}x^{2}+\sqrt{3}x=-\frac{\sqrt{3}}{4}(x - 2)^{2}+\sqrt{3}$,
∴当x = 2时,重叠部分面积有最大值,最大值是$\sqrt{3}$.