6.「2024云南昭通巧家期末,★☆」为庆祝第五个中国农民丰收节,宣传特色农产品,“迎盛会·庆丰收·促振兴”农特产品展销推荐会在白华生态农贸市场举行.某农户销售一种商品,成本价为每千克40元,按规定,该商品每千克的售价不低于成本价,且不高于60元.经调查,每天的销售量y(千克)与售价x(元/千克)满足一次函数关系,部分数据如下表:
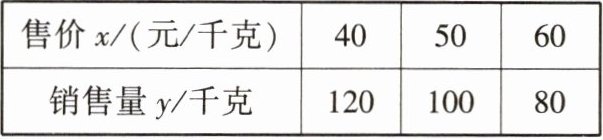
设销售该商品每天的利润为w(元),则w的最大值为(
A.1800
B.1600
C.1400
D.1200

设销售该商品每天的利润为w(元),则w的最大值为(
B
)A.1800
B.1600
C.1400
D.1200
答案:B 设y与x的函数关系式为$y=kx+b(k≠0)$,把$(40,120)$,$(50,100)$代入,得$\begin{cases}40k+b=120,\\50k+b=100,\end{cases}$解得$\begin{cases}k=-2,\\b=200,\end{cases}$$\therefore y=-2x+200$,根据题意,得$w=(x-40)y=(x-40)(-2x+200)=-2(x-70)^{2}+1800$,$\because -2<0$,$40≤x≤60$,$\therefore x=60$时,w取得最大值,$w_{最大}=-2×(60-70)^{2}+1800=1600$.故选B.
7.「2024四川南充中考,★☆」2024年五一假期期间,阆中古城景区某特产店销售A,B两类特产.A类特产进价为50元/件,B类特产进价为60元/件.已知购买1件A类特产和1件B类特产需132元,购买3件A类特产和5件B类特产需540元.
(1)求A类特产和B类特产每件的售价.
(2)A类特产供货充足,按原价销售每天可售出60件.市场调查反映,若每降价1元,每天可多售出10件(每件售价不低于进价).设每件A类特产降价x元,每天的销售量为y件,求y与x之间的函数关系式,并写出自变量x的取值范围.
(3)在(2)的条件下,由于B类特产供货紧张,每天只能购进100件且能按原价售完.设该店每天销售这两类特产的总利润为w元,求w与x的函数关系式,并求出每件A类特产降价多少元时总利润w最大,最大利润是多少元.(利润= 售价-进价)
(1)求A类特产和B类特产每件的售价.
(2)A类特产供货充足,按原价销售每天可售出60件.市场调查反映,若每降价1元,每天可多售出10件(每件售价不低于进价).设每件A类特产降价x元,每天的销售量为y件,求y与x之间的函数关系式,并写出自变量x的取值范围.
(3)在(2)的条件下,由于B类特产供货紧张,每天只能购进100件且能按原价售完.设该店每天销售这两类特产的总利润为w元,求w与x的函数关系式,并求出每件A类特产降价多少元时总利润w最大,最大利润是多少元.(利润= 售价-进价)
答案:解析 (1)设A类特产每件的售价为x元,则B类特产每件的售价为$(132-x)$元.$\therefore 3x+5(132-x)=540$.
$\therefore x=60$.$\therefore$B类特产每件的售价为$132-60=72$(元).
答:A类特产每件的售价为60元,B类特产每件的售价为72元.
(2)$y=10x+60(0≤x≤10)$.
(3)由题意得$w=(60-50-x)(10x+60)+100×(72-60)=-10x^{2}+40x+1800=-10(x-2)^{2}+1840$.
$\because -10<0$,$\therefore$当$x=2$时,w有最大值,为1840.
$\therefore$A类特产每件降价2元时,每天的销售利润最大,最大利润为1840元.
$\therefore x=60$.$\therefore$B类特产每件的售价为$132-60=72$(元).
答:A类特产每件的售价为60元,B类特产每件的售价为72元.
(2)$y=10x+60(0≤x≤10)$.
(3)由题意得$w=(60-50-x)(10x+60)+100×(72-60)=-10x^{2}+40x+1800=-10(x-2)^{2}+1840$.
$\because -10<0$,$\therefore$当$x=2$时,w有最大值,为1840.
$\therefore$A类特产每件降价2元时,每天的销售利润最大,最大利润为1840元.
8.新模型观念 某公司不断创新发展,生产销售某产品,该产品的销售量y(万件)与售价x(元/件)之间的函数关系式为$y= -x+22(6≤x≤16)$.
(1)当销售总额为120万元时,每件售价多少元?
每件售价为
(2)若总成本P(万元)与销售量y(万件)之间存在如图所示的变化趋势,当$6≤y<10$时,图象为一条线段(不含右端点),当$10≤y≤16$时,图象为抛物线$P= -\frac {1}{5}y^{2}+10y+10$的一部分,问售价为多少时,总利润最大?最大利润是多少?
当售价为
(1)当销售总额为120万元时,每件售价多少元?
每件售价为
10元或12元
.(2)若总成本P(万元)与销售量y(万件)之间存在如图所示的变化趋势,当$6≤y<10$时,图象为一条线段(不含右端点),当$10≤y≤16$时,图象为抛物线$P= -\frac {1}{5}y^{2}+10y+10$的一部分,问售价为多少时,总利润最大?最大利润是多少?
当售价为
16
元/件时,利润最大,最大利润是46
万元.答案:解析 (1)根据题意,得$x(-x+22)=120$,解得$x_{1}=10$,$x_{2}=12$,$\because 10$和12都在$6≤x≤16$内,$\therefore$每件售价为10元或12元.
(2)当$6≤y<10$时,$12<x≤16$,设$P=ay+n(a≠0)$,把$(6,50)$,$(10,90)$代入得$\begin{cases}50=6a+n,\\90=10a+n,\end{cases}$解得$\begin{cases}a=10,\\n=-10,\end{cases}$
$\therefore P=10y-10$,设总利润为w万元,则$w=yx-P=(-x+22)x-10(-x+22)+10=-x^{2}+32x-210=-(x-16)^{2}+46$,
$\because -1<0$,$12<x≤16$,$\therefore$当$x=16$时,w最大,最大值为46.当$10≤y≤16$时,$6≤x≤12$,$w=yx-P=(-x+22)x- [-\frac{1}{5}(-x+22)^{2}+10(-x+22)+10]=-\frac{4}{5}x^{2}+\frac{116}{5}x-\frac{666}{5}$,$\because$函数图象的对称轴为直线$x=-\frac{b}{2a}=\frac{29}{2}>12$,
$\therefore$当$x=12$时,w最大,最大值为30.$\because 46>30$,$\therefore$当售价为16元/件时,利润最大,最大利润是46万元.
(2)当$6≤y<10$时,$12<x≤16$,设$P=ay+n(a≠0)$,把$(6,50)$,$(10,90)$代入得$\begin{cases}50=6a+n,\\90=10a+n,\end{cases}$解得$\begin{cases}a=10,\\n=-10,\end{cases}$
$\therefore P=10y-10$,设总利润为w万元,则$w=yx-P=(-x+22)x-10(-x+22)+10=-x^{2}+32x-210=-(x-16)^{2}+46$,
$\because -1<0$,$12<x≤16$,$\therefore$当$x=16$时,w最大,最大值为46.当$10≤y≤16$时,$6≤x≤12$,$w=yx-P=(-x+22)x- [-\frac{1}{5}(-x+22)^{2}+10(-x+22)+10]=-\frac{4}{5}x^{2}+\frac{116}{5}x-\frac{666}{5}$,$\because$函数图象的对称轴为直线$x=-\frac{b}{2a}=\frac{29}{2}>12$,
$\therefore$当$x=12$时,w最大,最大值为30.$\because 46>30$,$\therefore$当售价为16元/件时,利润最大,最大利润是46万元.