1.「2025 内蒙古月考」下列说法中,不正确的是(
A.圆既是轴对称图形,又是中心对称图形
B.圆绕着它的圆心旋转任意角度,都能与自身重合
C.圆的对称轴有无数条,对称中心只有一个
D.圆的每一条直径都是它的对称轴
D
)A.圆既是轴对称图形,又是中心对称图形
B.圆绕着它的圆心旋转任意角度,都能与自身重合
C.圆的对称轴有无数条,对称中心只有一个
D.圆的每一条直径都是它的对称轴
答案:1.D 圆的每一条直径所在的直线都是它的对称轴,原说法错误.故选D.
2.如图,点 A,B 在$\odot O$上,直径$MN⊥AB$于点 C,下列结论中不一定成立的是(
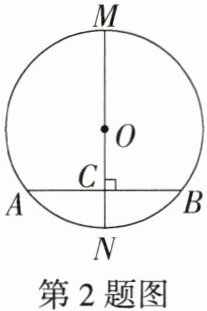
A.$AC= CB$
B.$OC= CN$
C.$\widehat {AN}= \widehat {BN}$
D.$\widehat {AM}= \widehat {BM}$
B
)
A.$AC= CB$
B.$OC= CN$
C.$\widehat {AN}= \widehat {BN}$
D.$\widehat {AM}= \widehat {BM}$
答案:2.B ∵点A,B在⊙O上,直径MN⊥AB于点C,∴AC=CB,$\overset{\frown}{AN}=\overset{\frown}{BN}$,$\overset{\frown}{AM}=\overset{\frown}{BM}$,故选项A,C,D不符合题意,OC 和CN不一定相等,故选项B符合题意.故选B.
3.「2024 湖南长沙中考」如图,在$\odot O$中,弦 AB 的长为8,圆心 O 到 AB 的距离$OE= 4$,则$\odot O$的半径长为(

A.4
B.$4\sqrt {2}$
C.5
D.$5\sqrt {2}$
B
)
A.4
B.$4\sqrt {2}$
C.5
D.$5\sqrt {2}$
答案:3.B 连接OA(图略),∵OE⊥AB,∴AE=EB=$\frac{1}{2}$AB=4,∴OA=$\sqrt{AE^{2}+OE^{2}}=\sqrt{4^{2}+4^{2}} = 4\sqrt{2}$,故⊙O的半径长为$4\sqrt{2}$.故选B.
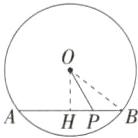
4.「2025 湖北黄石大冶期中」如图,$\odot O$的半径为 10,AB是$\odot O$的弦,$AB= 16$,点 P 在弦 AB 上,则线段OP 的最小值是____.


答案:
答案6
解析 如图,过点O作OH⊥AB于点H,连接OB,由垂径定理得HA=HB=$\frac{1}{2}$AB=8,∵OB=10,∴OH=$\sqrt{OB^{2}-HB^{2}} = 6$,由垂线段最短可知,当点P位于点H的位置时,线段OP有最小值,最小值是6.
答案6
解析 如图,过点O作OH⊥AB于点H,连接OB,由垂径定理得HA=HB=$\frac{1}{2}$AB=8,∵OB=10,∴OH=$\sqrt{OB^{2}-HB^{2}} = 6$,由垂线段最短可知,当点P位于点H的位置时,线段OP有最小值,最小值是6.

5.跨化学蒸馏瓶「2025 江苏盐城期中」如图所示的是一种用于液体蒸馏或分馏物质的玻璃容器——蒸馏瓶,其中球的半径为 5 cm,瓶内液体的最大深度$CD= 3cm$,则截面圆中弦 AB 的长为

$2\sqrt{21}$
cm.
答案:答案 $2\sqrt{21}$
解析 ∵OA=OD=5cm,CD=3cm,∴OC=5−3=2(cm),∴AC=$\sqrt{OA^{2}-OC^{2}}=\sqrt{5^{2}-2^{2}}=\sqrt{21}$(cm),由垂径定理可得AB=2AC=$2\sqrt{21}$cm.
解析 ∵OA=OD=5cm,CD=3cm,∴OC=5−3=2(cm),∴AC=$\sqrt{OA^{2}-OC^{2}}=\sqrt{5^{2}-2^{2}}=\sqrt{21}$(cm),由垂径定理可得AB=2AC=$2\sqrt{21}$cm.
6.学科方程特色思想「2025 辽宁大连中山期中」如图,$OA= OB$,AB 交$\odot O$于点 C,D,OE 是半径,且$OE⊥AB$于点 F.
(1)求证:$AC= BD$.
(2)若$CD= 10,EF= 3$,求$\odot O$的半径.

(1)求证:$AC= BD$.
(2)若$CD= 10,EF= 3$,求$\odot O$的半径.

答案:
解析 (1)证明:∵OA=OB,OE⊥AB于点F,∴AF=BF,∵OE是⊙O的半径,OE⊥AB,∴CF=DF,∴AF - CF=BF - DF,∴AC=BD.
(2)如图,连接OC,∵OE⊥AB,CD为⊙O的弦,∴CF=$\frac{1}{2}$CD=5,∠OFC = $90^{\circ}$,∴$CO^{2}=CF^{2}+OF^{2}$,设⊙O的半径是r,∴$r^{2}=5^{2}+(r - 3)^{2}$,解得$r=\frac{17}{3}$,∴⊙O的半径是$\frac{17}{3}$.

解析 (1)证明:∵OA=OB,OE⊥AB于点F,∴AF=BF,∵OE是⊙O的半径,OE⊥AB,∴CF=DF,∴AF - CF=BF - DF,∴AC=BD.
(2)如图,连接OC,∵OE⊥AB,CD为⊙O的弦,∴CF=$\frac{1}{2}$CD=5,∠OFC = $90^{\circ}$,∴$CO^{2}=CF^{2}+OF^{2}$,设⊙O的半径是r,∴$r^{2}=5^{2}+(r - 3)^{2}$,解得$r=\frac{17}{3}$,∴⊙O的半径是$\frac{17}{3}$.

7.「2024 河南洛阳伊滨期中」下列说法正确的是(
A.过弦的中点的直径平分弦所对的两条弧
B.弦的垂直平分线平分它所对的两条弧,但不一定过圆心
C.过弦的中点的直径垂直于弦
D.平分弦所对的两条弧的直径平分弦
D
)A.过弦的中点的直径平分弦所对的两条弧
B.弦的垂直平分线平分它所对的两条弧,但不一定过圆心
C.过弦的中点的直径垂直于弦
D.平分弦所对的两条弧的直径平分弦
答案:7.D A.过弦(不是直径)的中点的直径平分弦所对的两条弧,故A错误,不符合题意;
B.弦的垂直平分线平分它所对的两条弧,一定过圆心,故B错误,不符合题意;
C.过弦(不是直径)的中点的直径垂直于弦,故C错误,不符合题意;
D.平分弦所对的两条弧的直径平分弦,故D正确,符合题意.故选D.
B.弦的垂直平分线平分它所对的两条弧,一定过圆心,故B错误,不符合题意;
C.过弦(不是直径)的中点的直径垂直于弦,故C错误,不符合题意;
D.平分弦所对的两条弧的直径平分弦,故D正确,符合题意.故选D.
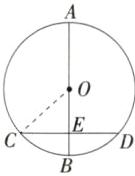
8.「2025 上海杨浦月考」如图,在圆 O 中,直径$AB= 10$,弦 CD 交 AB 于点 E,且$CE= DE$,若$BE= 2$,则

$CD= $____.

$CD= $____.
答案:
答案 8
解析 如图,连接OC,∵直径AB=10,∴OB=OC=5,∵BE=2,∴OE=OB - BE=5 - 2=3,∵CE=DE,∴OE⊥CD,∴CE=$\sqrt{OC^{2}-OE^{2}}=\sqrt{5^{2}-3^{2}} = 4$,∴CD=2CE=8.
答案 8
解析 如图,连接OC,∵直径AB=10,∴OB=OC=5,∵BE=2,∴OE=OB - BE=5 - 2=3,∵CE=DE,∴OE⊥CD,∴CE=$\sqrt{OC^{2}-OE^{2}}=\sqrt{5^{2}-3^{2}} = 4$,∴CD=2CE=8.

9.新考向尺规作图如图,AB 是$\odot O$的直径,点 P 是 AB 上一点,且点 P 是弦 CD 的中点.
(1)依题意画出弦 CD.(尺规作图,不写作法,保留作图痕迹)
(2)若$AP= 4,CD= 16$,求$\odot O$的半径.
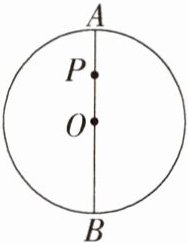
(1)依题意画出弦 CD.(尺规作图,不写作法,保留作图痕迹)
(2)若$AP= 4,CD= 16$,求$\odot O$的半径.

答案:
解析 (1)弦CD如图所示.
(2)如图,连接OD,∵点P是弦CD的中点,AB是⊙O的直径,CD=16,∴∠OPD = $90^{\circ}$,PD=$\frac{1}{2}$CD=8.设⊙O的半径为r,则OD=r,OP=OA - AP=r - 4,∵在Rt△ODP中,∠OPD = $90^{\circ}$,∴$OD^{2}=OP^{2}+PD^{2}$,即$r^{2}=(r - 4)^{2}+8^{2}$,解得r=10,即⊙O的半径为10.

解析 (1)弦CD如图所示.
(2)如图,连接OD,∵点P是弦CD的中点,AB是⊙O的直径,CD=16,∴∠OPD = $90^{\circ}$,PD=$\frac{1}{2}$CD=8.设⊙O的半径为r,则OD=r,OP=OA - AP=r - 4,∵在Rt△ODP中,∠OPD = $90^{\circ}$,∴$OD^{2}=OP^{2}+PD^{2}$,即$r^{2}=(r - 4)^{2}+8^{2}$,解得r=10,即⊙O的半径为10.
