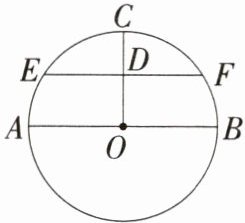
9. [2025 北京海淀月考,★☆]如图,已知 AB 是$\odot O$的直径,半径$OC⊥AB$,D 是 CO 的中点,若过点 D 的弦$EF// AB$,则下列结论正确的是 ( )
A.$\overset{\frown }{EC}= \overset{\frown }{AE}$
B.$\overset{\frown }{EC}= 2\overset{\frown }{AE}$
C.$\overset{\frown }{EF}= 3\overset{\frown }{AE}$
D.$\overset{\frown }{ABF}= 4\overset{\frown }{AE}$

A.$\overset{\frown }{EC}= \overset{\frown }{AE}$
B.$\overset{\frown }{EC}= 2\overset{\frown }{AE}$
C.$\overset{\frown }{EF}= 3\overset{\frown }{AE}$
D.$\overset{\frown }{ABF}= 4\overset{\frown }{AE}$
答案:
B 如图,连接 OE、OF、CE,$\because OC⊥AB$,$EF// AB$,$\therefore OC⊥EF$,$\therefore ∠ODE = 90^{\circ}$,又$\because D$是 CO 的中点,$\therefore CE = OE = OC$,$\therefore \triangle COE$是等边三角形,$\therefore ∠EOD = 60^{\circ}$,$\because EF// AB$,$\therefore ∠AOE = ∠OED = 90^{\circ} - ∠EOD = 30^{\circ}$,$\therefore \overset{\frown}{EC} = 2\overset{\frown}{AE}$,故选项 A 错误,选项 B 正确;易得$∠EOF = 120^{\circ}$,$\therefore \overset{\frown}{EF} = 4\overset{\frown}{AE}$,故选项 C 错误;$\because \overset{\frown}{ABF}$所对的圆心角的度数为$210^{\circ}$,$\therefore \overset{\frown}{ABF} = 7\overset{\frown}{AE}$,故选项 D 错误.故选 B.
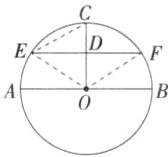
B 如图,连接 OE、OF、CE,$\because OC⊥AB$,$EF// AB$,$\therefore OC⊥EF$,$\therefore ∠ODE = 90^{\circ}$,又$\because D$是 CO 的中点,$\therefore CE = OE = OC$,$\therefore \triangle COE$是等边三角形,$\therefore ∠EOD = 60^{\circ}$,$\because EF// AB$,$\therefore ∠AOE = ∠OED = 90^{\circ} - ∠EOD = 30^{\circ}$,$\therefore \overset{\frown}{EC} = 2\overset{\frown}{AE}$,故选项 A 错误,选项 B 正确;易得$∠EOF = 120^{\circ}$,$\therefore \overset{\frown}{EF} = 4\overset{\frown}{AE}$,故选项 C 错误;$\because \overset{\frown}{ABF}$所对的圆心角的度数为$210^{\circ}$,$\therefore \overset{\frown}{ABF} = 7\overset{\frown}{AE}$,故选项 D 错误.故选 B.

10. [学科特色 方程思想 ★☆]如图,AB 为$\odot O$的直径,点 D 是$\overset{\frown }{AC}$的中点,过点 D 作$DE⊥AB$于点 E,延长 DE 交$\odot O$于点 F.若$AC= 4\sqrt {3}$,$AE= 2$,则$\odot O$的直径为 (

A.$8\sqrt {3}$
B.8
C.10
D.$8\sqrt {2}$
B
)
A.$8\sqrt {3}$
B.8
C.10
D.$8\sqrt {2}$
答案:B 连接 OF(图略),$\because DE⊥AB$,$\therefore DE = EF$,$\overset{\frown}{AD} = \overset{\frown}{AF}$,$\because$点 D 是$\overset{\frown}{AC}$的中点,$\therefore \overset{\frown}{AD} = \overset{\frown}{CD}$,$\therefore \overset{\frown}{AC} = \overset{\frown}{DF}$,$\therefore DF = AC = 4\sqrt{3}$,$\therefore EF = \frac{1}{2}DF = 2\sqrt{3}$,设$OA = OF = x$,$\therefore OE = x - 2$,在$Rt\triangle OEF$中,$x^{2} = (2\sqrt{3})^{2} + (x - 2)^{2}$,解得$x = 4$,$\therefore AB = 2x = 8$.故选 B.
11. [★☆]如图,点 A、B、C、D 在$\odot O$上,且$\overset{\frown }{AD}= \overset{\frown }{BC}$,E 是 AB 延长线上一点,且$BE= AB$,F 是 EC 的中点,若$BF= 6cm$,则$BD= $______

12
cm.
答案:答案 12
解析 连接 AC(图略),$\because F$是 EC 的中点,$\therefore CF = EF$,$\because BE = AB$,$\therefore BF$是$\triangle EAC$的中位线,$\therefore BF = \frac{1}{2}AC$,$\because \overset{\frown}{AD} = \overset{\frown}{BC}$,$\therefore \overset{\frown}{AD} + \overset{\frown}{AB} = \overset{\frown}{BC} + \overset{\frown}{AB}$,$\therefore \overset{\frown}{DB} = \overset{\frown}{AC}$,$\therefore BD = AC$,$\therefore BF = \frac{1}{2}BD$,$\therefore BD = 2BF = 12cm$.
解析 连接 AC(图略),$\because F$是 EC 的中点,$\therefore CF = EF$,$\because BE = AB$,$\therefore BF$是$\triangle EAC$的中位线,$\therefore BF = \frac{1}{2}AC$,$\because \overset{\frown}{AD} = \overset{\frown}{BC}$,$\therefore \overset{\frown}{AD} + \overset{\frown}{AB} = \overset{\frown}{BC} + \overset{\frown}{AB}$,$\therefore \overset{\frown}{DB} = \overset{\frown}{AC}$,$\therefore BD = AC$,$\therefore BF = \frac{1}{2}BD$,$\therefore BD = 2BF = 12cm$.
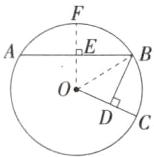
12. [2025 江苏泰州姜堰期中,★☆]如图,在$\odot O$中,$\overset{\frown }{AB}= 2\overset{\frown }{BC}$,且$BD⊥OC$,垂足为 D.若$AB= 8$,$CD= 2$,则$\odot O$的半径为______.


答案:
答案 5
解析 如图,过点 O 作 AB 的垂线交 AB 于点 E,交$\overset{\frown}{AB}$于点 F,连接 OB.$\because OF⊥AB$,$AB = 8$,$\therefore \overset{\frown}{AF} = \overset{\frown}{BF} = \frac{1}{2}\overset{\frown}{AB}$,$AE = BE = \frac{1}{2}AB = \frac{1}{2}×8 = 4$,$\because \overset{\frown}{AB} = 2\overset{\frown}{BC}$,$\therefore \overset{\frown}{BC} = \frac{1}{2}\overset{\frown}{AB} = \overset{\frown}{BF}$,$\therefore ∠BOC = ∠BOF$,即 OB 平分$∠COF$,$\because BD⊥OC$,$\therefore BD = BE = 4$,设$\odot O$的半径为 r,则$OB = OC = r$,$\because CD = 2$,$\therefore OD = OC - CD = r - 2$,在$Rt\triangle BOD$中,由勾股定理,得$BD^{2} + OD^{2} = OB^{2}$,$\therefore 4^{2} + (r - 2)^{2} = r^{2}$,$\therefore r = 5$,$\therefore \odot O$的半径为 5.
答案 5
解析 如图,过点 O 作 AB 的垂线交 AB 于点 E,交$\overset{\frown}{AB}$于点 F,连接 OB.$\because OF⊥AB$,$AB = 8$,$\therefore \overset{\frown}{AF} = \overset{\frown}{BF} = \frac{1}{2}\overset{\frown}{AB}$,$AE = BE = \frac{1}{2}AB = \frac{1}{2}×8 = 4$,$\because \overset{\frown}{AB} = 2\overset{\frown}{BC}$,$\therefore \overset{\frown}{BC} = \frac{1}{2}\overset{\frown}{AB} = \overset{\frown}{BF}$,$\therefore ∠BOC = ∠BOF$,即 OB 平分$∠COF$,$\because BD⊥OC$,$\therefore BD = BE = 4$,设$\odot O$的半径为 r,则$OB = OC = r$,$\because CD = 2$,$\therefore OD = OC - CD = r - 2$,在$Rt\triangle BOD$中,由勾股定理,得$BD^{2} + OD^{2} = OB^{2}$,$\therefore 4^{2} + (r - 2)^{2} = r^{2}$,$\therefore r = 5$,$\therefore \odot O$的半径为 5.

13. [2025 贵州贵阳期中,★☆]如图,AB 为$\odot O$的弦,半径 OC,OD 分别交 AB 于点 E,F,且$\overset{\frown }{AC}= \overset{\frown }{DB}$.
(1)求证:$AE= BF$.
(2)作半径$ON⊥AB$于点 M,若$AB= 12$,$MN= 3$,求 OM 的长.

(1)求证:$AE= BF$.
(2)作半径$ON⊥AB$于点 M,若$AB= 12$,$MN= 3$,求 OM 的长.

答案:
解析 (1)证明:连接 OA,OB,如图.$\because OA = OB$,$\therefore ∠OAB = ∠OBA$,$\because \overset{\frown}{AC} = \overset{\frown}{BD}$,$\therefore ∠AOE = ∠BOF$,在$\triangle AOE$和$\triangle BOF$中,$\begin{cases}∠OAE = ∠OBF,\\OA = OB,\\∠AOE = ∠BOF,\end{cases}$ $\therefore \triangle AOE ≌ \triangle BOF(ASA)$,$\therefore AE = BF$.(2)连接 OA,如图.$\because OM⊥AB$,$\therefore AM = \frac{1}{2}AB = 6$,设$OM = x$,则$OA = ON = x + 3$,在$Rt\triangle AOM$中,由勾股定理得$6^{2} + x^{2} = (x + 3)^{2}$,解得$x = 4.5$,$\therefore OM = 4.5$.

解析 (1)证明:连接 OA,OB,如图.$\because OA = OB$,$\therefore ∠OAB = ∠OBA$,$\because \overset{\frown}{AC} = \overset{\frown}{BD}$,$\therefore ∠AOE = ∠BOF$,在$\triangle AOE$和$\triangle BOF$中,$\begin{cases}∠OAE = ∠OBF,\\OA = OB,\\∠AOE = ∠BOF,\end{cases}$ $\therefore \triangle AOE ≌ \triangle BOF(ASA)$,$\therefore AE = BF$.(2)连接 OA,如图.$\because OM⊥AB$,$\therefore AM = \frac{1}{2}AB = 6$,设$OM = x$,则$OA = ON = x + 3$,在$Rt\triangle AOM$中,由勾股定理得$6^{2} + x^{2} = (x + 3)^{2}$,解得$x = 4.5$,$\therefore OM = 4.5$.

14. [新课标 推理能力]如图,点 C、D 三等分以 O 为圆心的$\overset{\frown }{MN}$,连接 MN、CD、OC、OD、OM,下列结论错误的是 ( )

A.$∠COM= ∠COD$
B.若$OM= MN$,则$∠COD= 20^{\circ }$
C.$MN// CD$
D.$MN= 3CD$

A.$∠COM= ∠COD$
B.若$OM= MN$,则$∠COD= 20^{\circ }$
C.$MN// CD$
D.$MN= 3CD$
答案:
D 如图,连接 ON、MC、DN,过点 O 作$OE⊥CD$,交$\overset{\frown}{CD}$于点 E,$\because \overset{\frown}{CM} = \overset{\frown}{CD}$,$\therefore ∠COM = ∠COD$,故选项 A 结论正确.当$OM = MN$时,$\because OM = ON$,$\therefore OM = ON = MN$,$\therefore \triangle OMN$为等边三角形,$\therefore ∠MON = 60^{\circ}$,$\because \overset{\frown}{CM} = \overset{\frown}{CD} = \overset{\frown}{DN}$,$\therefore ∠COM = ∠COD = ∠DON$,$\therefore ∠COD = 20^{\circ}$,故选项 B 结论正确.$\because OE⊥CD$,$\therefore \overset{\frown}{CE} = \overset{\frown}{DE}$,$\therefore \overset{\frown}{ME} = \overset{\frown}{NE}$,$\therefore OE⊥MN$,$\therefore MN// CD$,故选项 C 结论正确.$\because \overset{\frown}{CM} = \overset{\frown}{CD} = \overset{\frown}{DN}$,$\therefore MC = CD = DN$,$\because MC + CD + DN > MN$,$\therefore MN < 3CD$,故选项 D 结论错误.故选 D.

D 如图,连接 ON、MC、DN,过点 O 作$OE⊥CD$,交$\overset{\frown}{CD}$于点 E,$\because \overset{\frown}{CM} = \overset{\frown}{CD}$,$\therefore ∠COM = ∠COD$,故选项 A 结论正确.当$OM = MN$时,$\because OM = ON$,$\therefore OM = ON = MN$,$\therefore \triangle OMN$为等边三角形,$\therefore ∠MON = 60^{\circ}$,$\because \overset{\frown}{CM} = \overset{\frown}{CD} = \overset{\frown}{DN}$,$\therefore ∠COM = ∠COD = ∠DON$,$\therefore ∠COD = 20^{\circ}$,故选项 B 结论正确.$\because OE⊥CD$,$\therefore \overset{\frown}{CE} = \overset{\frown}{DE}$,$\therefore \overset{\frown}{ME} = \overset{\frown}{NE}$,$\therefore OE⊥MN$,$\therefore MN// CD$,故选项 C 结论正确.$\because \overset{\frown}{CM} = \overset{\frown}{CD} = \overset{\frown}{DN}$,$\therefore MC = CD = DN$,$\because MC + CD + DN > MN$,$\therefore MN < 3CD$,故选项 D 结论错误.故选 D.

15. [新课标 几何直观 2025 河南驻马店西平期中]如图,CD 是$\odot O$的直径,点 A 是半圆上靠近点 D 的一个三等分点,B 是$\overset{\frown }{AD}$的中点,P 为直线 CD 上的一个动点,当$CD= 4$时,$AP+BP$的最小值为______.


答案:
答案 $2\sqrt{2}$
解析 如图,作点 A 关于 CD 的对称点$A'$,连接$A'B$,交 CD 于点 P,此时$PA + PB$的值最小,最小值为$A'B$的长,连接$OA'$,OB,$\because$点 A 与$A'$关于 CD 对称,点 A 是半圆上靠近点 D 的一个三等分点,$\therefore PA = PA'$,$∠A'OD = ∠AOD = 60^{\circ}$,$\because$点 B 是$\overset{\frown}{AD}$的中点,$\therefore ∠BOD = 30^{\circ}$,$\therefore ∠A'OB = ∠A'OD + ∠BOD = 90^{\circ}$,易知$OB = OA' = 2$,$\therefore A'B = 2\sqrt{2}$,$\therefore PA + PB = PA' + PB = A'B = 2\sqrt{2}$,$\therefore AP + BP$的最小值为$2\sqrt{2}$.

答案 $2\sqrt{2}$
解析 如图,作点 A 关于 CD 的对称点$A'$,连接$A'B$,交 CD 于点 P,此时$PA + PB$的值最小,最小值为$A'B$的长,连接$OA'$,OB,$\because$点 A 与$A'$关于 CD 对称,点 A 是半圆上靠近点 D 的一个三等分点,$\therefore PA = PA'$,$∠A'OD = ∠AOD = 60^{\circ}$,$\because$点 B 是$\overset{\frown}{AD}$的中点,$\therefore ∠BOD = 30^{\circ}$,$\therefore ∠A'OB = ∠A'OD + ∠BOD = 90^{\circ}$,易知$OB = OA' = 2$,$\therefore A'B = 2\sqrt{2}$,$\therefore PA + PB = PA' + PB = A'B = 2\sqrt{2}$,$\therefore AP + BP$的最小值为$2\sqrt{2}$.
