1.一条弧所对的圆心角为$135^{\circ }$,弧长等于半径为3 cm的圆的周长的5倍,则这条弧所在圆的半径为(
A.45 cm
B.40 cm
C.35 cm
D.30 cm
40
)A.45 cm
B.40 cm
C.35 cm
D.30 cm
答案:B 设这条弧所在圆的半径为 $ r $ cm,由题意得 $ \frac{135\pi r}{180} = 2\pi \times 3 \times 5 $,解得 $ r = 40 $。
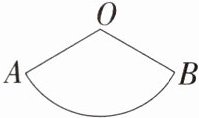
2.「2024四川成都中考」如图,在扇形AOB中,$OA= 6$,$∠AOB= 120^{\circ }$,则$\overset{\frown }{AB}$的长为
4π
.
答案:答案 $ 4\pi $
解析 由题意得 $ \overset{\frown}{AB} $ 的长 $ = \frac{120\pi \times 6}{180} = 4\pi $。
解析 由题意得 $ \overset{\frown}{AB} $ 的长 $ = \frac{120\pi \times 6}{180} = 4\pi $。
3.「2024云南文山广南模拟」在一个半径为27 cm的圆上,截取一段长度为$21π$ cm的圆弧,则这段圆弧所对的圆心角的度数为
$140^{\circ} $
.答案:答案 $ 140^{\circ} $
解析 设这段圆弧所对的圆心角的度数为 $ n^{\circ} $,由题意得,$ 21\pi = \frac{n\pi \times 27}{180} $,解得 $ n = 140 $,∴ 这段圆弧所对的圆心角的度数为 $ 140^{\circ} $。
解析 设这段圆弧所对的圆心角的度数为 $ n^{\circ} $,由题意得,$ 21\pi = \frac{n\pi \times 27}{180} $,解得 $ n = 140 $,∴ 这段圆弧所对的圆心角的度数为 $ 140^{\circ} $。
4.「2023上海浦东新区期末」小丽家时钟的分针长5 cm,时针的长度是分针的$\frac {3}{5}$,从下午1点到下午5点,时针针尖走过
$2\pi$
cm.答案:答案 $ 2\pi $
解析 由题意得,时针的长度为 $ 5 \times \frac{3}{5} = 3 $ (cm),时针从下午 1 点到下午 5 点旋转的度数为 $ 120^{\circ} $,∴ 从下午 1 点到下午 5 点,时针针尖走过的路径为 $ \frac{120\pi \times 3}{180} = 2\pi $ (cm)。
解析 由题意得,时针的长度为 $ 5 \times \frac{3}{5} = 3 $ (cm),时针从下午 1 点到下午 5 点旋转的度数为 $ 120^{\circ} $,∴ 从下午 1 点到下午 5 点,时针针尖走过的路径为 $ \frac{120\pi \times 3}{180} = 2\pi $ (cm)。
5.跨物理滑轮「2025江苏宿迁泗阳期中」物理实验课上,同学们分组研究定滑轮“可以改变用力的方向,但不能省力”时,爱动脑筋的小颖发现:重物上升时,滑轮上点A的位置在不断改变,已知滑轮的半径为12 cm,当重物上升$4π$ cm时,滑轮上点A转过的度数为____
60°
.答案:答案 $ 60^{\circ} $
解析 设滑轮上点 $ A $ 转过的度数为 $ n^{\circ} $,由题意可知,点 $ A $ 转过的弧长为 $ 4\pi $ cm,∴ $ \frac{n\pi \times 12}{180} = 4\pi $,解得 $ n = 60 $,∴ 滑轮上点 $ A $ 转过的度数为 $ 60^{\circ} $。
解析 设滑轮上点 $ A $ 转过的度数为 $ n^{\circ} $,由题意可知,点 $ A $ 转过的弧长为 $ 4\pi $ cm,∴ $ \frac{n\pi \times 12}{180} = 4\pi $,解得 $ n = 60 $,∴ 滑轮上点 $ A $ 转过的度数为 $ 60^{\circ} $。
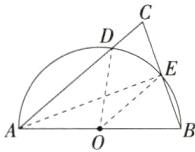
6.「2024四川广安中考,」如图,在等腰三角形ABC中,$AB= AC= 10$,$∠C= 70^{\circ }$,以AB为直径作半圆,与AC,BC分别相交于点D,E,则$\overset{\frown }{DE}$的长度为( )

A.$\frac {π}{9}$
B.$\frac {5π}{9}$
C.$\frac {10π}{9}$
D.$\frac {25π}{9}$

A.$\frac {π}{9}$
B.$\frac {5π}{9}$
C.$\frac {10π}{9}$
D.$\frac {25π}{9}$
答案:
C 如图,连接 $ OD $,$ OE $,$ AE $,
∵ $ AB $ 为半圆的直径,∴ $ \angle AEB = 90^{\circ} $,即 $ AE \perp BC $,
又 ∵ $ AB = AC $,∴ $ AE $ 平分 $ \angle CAB $,$ \angle ABC = \angle C = 70^{\circ} $,
在 $ \triangle ABC $ 中,$ \angle CAB = 180^{\circ} - \angle ABC - \angle C = 180^{\circ} - 70^{\circ} - 70^{\circ} = 40^{\circ} $,∴ $ \angle DAE = \frac{1}{2} \angle CAB = 20^{\circ} $,
∵ $ \overset{\frown}{DE} = \overset{\frown}{DE} $,∴ $ \angle DOE = 2 \angle DAE = 40^{\circ} $,
∵ $ AB = 10 $,∴ $ OD = OA = 5 $,
∴ $ \overset{\frown}{DE} $ 的长度为 $ \frac{40\pi \times 5}{180} = \frac{10\pi}{9} $,故选 C。
C 如图,连接 $ OD $,$ OE $,$ AE $,
∵ $ AB $ 为半圆的直径,∴ $ \angle AEB = 90^{\circ} $,即 $ AE \perp BC $,
又 ∵ $ AB = AC $,∴ $ AE $ 平分 $ \angle CAB $,$ \angle ABC = \angle C = 70^{\circ} $,
在 $ \triangle ABC $ 中,$ \angle CAB = 180^{\circ} - \angle ABC - \angle C = 180^{\circ} - 70^{\circ} - 70^{\circ} = 40^{\circ} $,∴ $ \angle DAE = \frac{1}{2} \angle CAB = 20^{\circ} $,
∵ $ \overset{\frown}{DE} = \overset{\frown}{DE} $,∴ $ \angle DOE = 2 \angle DAE = 40^{\circ} $,
∵ $ AB = 10 $,∴ $ OD = OA = 5 $,
∴ $ \overset{\frown}{DE} $ 的长度为 $ \frac{40\pi \times 5}{180} = \frac{10\pi}{9} $,故选 C。

7.「2024内蒙古兴安盟、呼伦贝尔中考,」为了促进城乡协调发展,实现共同富裕,某乡镇计划修建公路.如图,$\overset{\frown }{AB}与\overset{\frown }{CD}$是公路弯道的外、内边线,它们有共同的圆心O,所对的圆心角都是$72^{\circ }$,点A,C,O在同一条直线上,公路弯道外侧边线比内侧边线多36米,则公路宽AC的长是____
28.7
米.(π取3.14,计算结果精确到0.1)答案:答案 $ 28.7 $
解析 由题意得 $ \frac{72\pi \cdot OA}{180} - \frac{72\pi \cdot OC}{180} = 36 $,∴ $ OA - OC = \frac{90}{\pi} \approx 28.7 $ (米) ∴ $ AC = OA - OC = 28.7 $ 米。
解析 由题意得 $ \frac{72\pi \cdot OA}{180} - \frac{72\pi \cdot OC}{180} = 36 $,∴ $ OA - OC = \frac{90}{\pi} \approx 28.7 $ (米) ∴ $ AC = OA - OC = 28.7 $ 米。
8.「2024吉林长春中考,」一块含$30^{\circ }$角的直角三角尺ABC按如图所示的方式摆放,边AB在直线l上,$AB= 12$ cm.现将该三角尺绕点B顺时针旋转,使点C的对应点$C'$落在直线l上,则点A经过的路径长至少为

8π
cm.(结果保留π)
答案:答案 $ 8\pi $
解析 由题意得,点 $ A $ 经过的路径是以 $ B $ 为圆心的弧 $ AA' $。∵ $ \angle CAB = 30^{\circ} $,$ \angle C = 90^{\circ} $,∴ $ \angle ABC = 60^{\circ} $,∴ $ \angle A'BC' = 60^{\circ} $,∴ $ \angle ABA' = 120^{\circ} $,∴ 弧 $ AA' $ 的长度为 $ \frac{120 \times \pi \times 12}{180} = 8\pi $ (cm)。
解析 由题意得,点 $ A $ 经过的路径是以 $ B $ 为圆心的弧 $ AA' $。∵ $ \angle CAB = 30^{\circ} $,$ \angle C = 90^{\circ} $,∴ $ \angle ABC = 60^{\circ} $,∴ $ \angle A'BC' = 60^{\circ} $,∴ $ \angle ABA' = 120^{\circ} $,∴ 弧 $ AA' $ 的长度为 $ \frac{120 \times \pi \times 12}{180} = 8\pi $ (cm)。
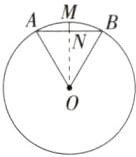
9.新考向数学文化「2024山东潍坊模拟,」《梦溪笔谈》是我国古代科技著作,其中记录了计算圆弧长度的“会圆术”.如图,$\overset{\frown }{AB}$是以点O为圆心,OA长为半径的圆弧,N是AB的中点,$MN⊥AB$.“会圆术”给出$\overset{\frown }{AB}$的长l的近似值计算公式:$l= AB+\frac {MN^{2}}{OA}$.当$OA= 4$,$∠AOB= 60^{\circ }$时,l的值为____.


答案:
答案 $ 11 - 4\sqrt{3} $
解析 连接 $ ON $,∵ $ OA = OB $,$ \angle AOB = 60^{\circ} $,∴ $ \triangle OAB $ 是等边三角形,∴ $ AB = OA = 4 $,∵ $ N $ 是 $ AB $ 的中点,∴ $ ON \perp AB $,∵ $ MN \perp AB $,∴ $ M $、$ N $、$ O $ 共线,由 $ \angle AOB = 60^{\circ} $ 得 $ \angle AON = 30^{\circ} $,∴ $ AN = \frac{1}{2} OA = 2 $,∴ $ ON = \sqrt{OA^{2} - AN^{2}} = 2\sqrt{3} $,∵ $ OM = OA = 4 $,∴ $ MN = OM - ON = 4 - 2\sqrt{3} $,∴ $ l = AB + \frac{MN^{2}}{OA} = 4 + \frac{(4 - 2\sqrt{3})^{2}}{4} = 11 - 4\sqrt{3} $。
答案 $ 11 - 4\sqrt{3} $
解析 连接 $ ON $,∵ $ OA = OB $,$ \angle AOB = 60^{\circ} $,∴ $ \triangle OAB $ 是等边三角形,∴ $ AB = OA = 4 $,∵ $ N $ 是 $ AB $ 的中点,∴ $ ON \perp AB $,∵ $ MN \perp AB $,∴ $ M $、$ N $、$ O $ 共线,由 $ \angle AOB = 60^{\circ} $ 得 $ \angle AON = 30^{\circ} $,∴ $ AN = \frac{1}{2} OA = 2 $,∴ $ ON = \sqrt{OA^{2} - AN^{2}} = 2\sqrt{3} $,∵ $ OM = OA = 4 $,∴ $ MN = OM - ON = 4 - 2\sqrt{3} $,∴ $ l = AB + \frac{MN^{2}}{OA} = 4 + \frac{(4 - 2\sqrt{3})^{2}}{4} = 11 - 4\sqrt{3} $。
