1.「2025江苏无锡惠山期中」下列说法中正确的是 (
A.三个点确定一个圆
B.长度相等的弧是等弧
C.直径所对的圆周角是直角
D.正五边形是中心对称图形
C
)A.三个点确定一个圆
B.长度相等的弧是等弧
C.直径所对的圆周角是直角
D.正五边形是中心对称图形
答案:C A. 不在同一直线上的三个点确定一个圆, 不符合题意; B. 在同圆或等圆中, 长度相等的弧是等弧, 不符合题意; C. 直径所对的圆周角是直角, 正确, 符合题意; D. 正五边形不是中心对称图形, 不符合题意. 故选 C.
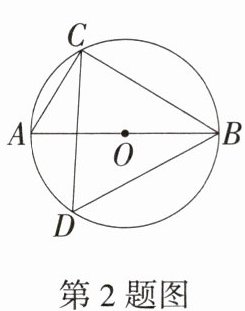
2.「2024四川宜宾中考」如图,AB是$\odot O$的直径,若$∠CDB= 60^{\circ }$,则$∠ABC$的度数等于 (
A.$30^{\circ }$
B.$45^{\circ }$
C.$60^{\circ }$
D.$90^{\circ }$
A
)
A.$30^{\circ }$
B.$45^{\circ }$
C.$60^{\circ }$
D.$90^{\circ }$
答案:A ∵ AB 是⊙O 的直径, ∴ ∠ACB = 90°, ∵ ∠CDB = 60°, ∴ ∠A = ∠CDB = 60°, ∴ ∠ABC = 90° - ∠A = 30°. 故选 A.
3.「2024吉林中考」如图,四边形ABCD内接于$\odot O$,过点B作$BE// AD$,交CD于点E.若$∠BEC= 50^{\circ }$,则$∠ABC$的度数是 (

A.$50^{\circ }$
B.$100^{\circ }$
C.$130^{\circ }$
D.$150^{\circ }$
C
)
A.$50^{\circ }$
B.$100^{\circ }$
C.$130^{\circ }$
D.$150^{\circ }$
答案:C ∵ BE // AD, ∴ ∠ADC = ∠BEC = 50°, ∵ 四边形 ABCD 内接于⊙O, ∴ ∠ABC = 180° - ∠ADC = 130°. 故选 C.
4.「2025湖北武汉江汉期中」在平面直角坐标系中,点P的坐标为$(3,-4)$,以P为圆心,4个单位长度为半径作圆,下列说法正确的是 (
A.原点O在$\odot P$内
B.原点O在$\odot P$上
C.$\odot P$与x轴相切,与y轴相交
D.$\odot P$与y轴相切,与x轴相交
C
)A.原点O在$\odot P$内
B.原点O在$\odot P$上
C.$\odot P$与x轴相切,与y轴相交
D.$\odot P$与y轴相切,与x轴相交
答案:C ∵ 点 P 的坐标为(3, -4), ∴ 点 P 到 x 轴的距离为 4, 到 y 轴的距离为 3, 到原点的距离为 $\sqrt{3^{2}+4^{2}} = 5$, ∵ 以 P 为圆心, 4 个单位长度为半径作圆, ∴ 原点 O 在⊙P 外, ⊙P 与 x 轴相切, 与 y 轴相交, 故选项 A, B, D 不符合题意, 选项 C 符合题意. 故选 C.
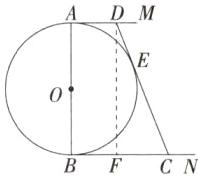
5.「2025浙江台州三门月考」如图,$\odot O$的直径AB的长度为定值a,AM和BN是它的两条切线,DE与$\odot O$相切于点E,并与AM,BN分别相交于点D,C,设$AD= x,BC= y$,当x,y的值变化时,下列代数式的值不变的是 ( )

A.$x-y$
B.$x+y$
C.xy
D.$x^{2}+y^{2}$

A.$x-y$
B.$x+y$
C.xy
D.$x^{2}+y^{2}$
答案:
C 如图, 作 DF ⊥ BN 于 F. ∵ AM, BN 与⊙O 切于点 A, B, ∴ AB ⊥ AM, AB ⊥ BN, 又 ∵ DF ⊥ BN, ∴ ∠BAD = ∠ABC = ∠BFD = 90°, ∴ 四边形 ABFD 是矩形, ∴ BF = AD = x, DF = AB = a, ∵ BC = y, ∴ FC = BC - BF = y - x. ∵ DE 切⊙O 于 E, ∴ DE = DA = x, CE = CB = y, 则 DC = DE + CE = x + y, 在 Rt△DFC 中, 由勾股定理得 $(x + y)^{2} = (y - x)^{2} + a^{2}$, ∴ $xy = \frac{a^{2}}{4}$, ∴ 代数式的值不变的是 xy. 故选 C.
C 如图, 作 DF ⊥ BN 于 F. ∵ AM, BN 与⊙O 切于点 A, B, ∴ AB ⊥ AM, AB ⊥ BN, 又 ∵ DF ⊥ BN, ∴ ∠BAD = ∠ABC = ∠BFD = 90°, ∴ 四边形 ABFD 是矩形, ∴ BF = AD = x, DF = AB = a, ∵ BC = y, ∴ FC = BC - BF = y - x. ∵ DE 切⊙O 于 E, ∴ DE = DA = x, CE = CB = y, 则 DC = DE + CE = x + y, 在 Rt△DFC 中, 由勾股定理得 $(x + y)^{2} = (y - x)^{2} + a^{2}$, ∴ $xy = \frac{a^{2}}{4}$, ∴ 代数式的值不变的是 xy. 故选 C.

6.「2025湖南长沙雨花月考」如图,点E是$\triangle ABC$的内心,AE的延长线和$\triangle ABC$的外接圆相交于点D,与BC相交于点G,则下列结论:①$∠BAD= ∠CAD$;②若点G为BC的中点,则$∠BGD= 90^{\circ }$;③连接BE,CE,若$∠BAC= 40^{\circ }$,则$∠BEC= 140^{\circ }$;④$BD= DE$.其中一定正确的个数是 ( )

A.4
B.3
C.2
D.1

A.4
B.3
C.2
D.1
答案:
B ∵ 点 E 是 △ABC 的内心, ∴ AD 平分 ∠BAC, ∴ ∠BAD = ∠CAD, 故①正确; 如图, 设 △ABC 外接圆圆心为 O, 连接 OD, 则 OD 垂直平分 BC, 若点 G 为 BC 的中点, 则点 G 为 OD 与 BC 的交点, 即 ∠BGD = 90°, 故②正确; 若 ∠BAC = 40°, 则 ∠ABC + ∠ACB = 180° - ∠BAC = 140°, ∵ 点 E 是 △ABC 的内心, ∴ ∠EBC = ∠ABE = $\frac{1}{2}$∠ABC, ∠ECB = ∠ACE = $\frac{1}{2}$∠ACB, ∴ ∠BEC = 180° - (∠EBC + ∠ECB) = 180° - $\frac{1}{2}$(∠ABC + ∠ACB) = 180° - $\frac{1}{2}$×140° = 110°, 故③错误; ∵ ∠BAD = ∠CAD, ∴ $\overparen{BD} = \overparen{CD}$, ∴ ∠DBC = ∠BAD, ∵ ∠DBE = ∠DBC + ∠EBC, ∠DEB = ∠BAD + ∠ABE, ∴ ∠DBE = ∠DEB, ∴ BD = DE, 故④正确. 综上, 正确的有 3 个. 故选 B.

B ∵ 点 E 是 △ABC 的内心, ∴ AD 平分 ∠BAC, ∴ ∠BAD = ∠CAD, 故①正确; 如图, 设 △ABC 外接圆圆心为 O, 连接 OD, 则 OD 垂直平分 BC, 若点 G 为 BC 的中点, 则点 G 为 OD 与 BC 的交点, 即 ∠BGD = 90°, 故②正确; 若 ∠BAC = 40°, 则 ∠ABC + ∠ACB = 180° - ∠BAC = 140°, ∵ 点 E 是 △ABC 的内心, ∴ ∠EBC = ∠ABE = $\frac{1}{2}$∠ABC, ∠ECB = ∠ACE = $\frac{1}{2}$∠ACB, ∴ ∠BEC = 180° - (∠EBC + ∠ECB) = 180° - $\frac{1}{2}$(∠ABC + ∠ACB) = 180° - $\frac{1}{2}$×140° = 110°, 故③错误; ∵ ∠BAD = ∠CAD, ∴ $\overparen{BD} = \overparen{CD}$, ∴ ∠DBC = ∠BAD, ∵ ∠DBE = ∠DBC + ∠EBC, ∠DEB = ∠BAD + ∠ABE, ∴ ∠DBE = ∠DEB, ∴ BD = DE, 故④正确. 综上, 正确的有 3 个. 故选 B.

7.「2023江西南昌青山湖期末」若用反证法证明“圆的切线垂直于过切点的半径”,第一步是提出假设:
圆的切线不垂直于过切点的半径
.答案:答案 圆的切线不垂直于过切点的半径
8.「2024山东烟台中考」如图,在边长为6的正六边形ABCDEF中,以点F为圆心,以FB的长为半径作$\overset{\frown }{BD}$,剪下图中阴影部分做一个圆锥的侧面,则这个圆锥的底面半径为______.


答案:
答案 $\sqrt{3}$
解析 ∵ 多边形 ABCDEF 是正六边形, ∴ ∠BAF = ∠AFE = $\frac{(6 - 2)×180°}{6} = 120°$, AB = AF, ∴ ∠AFB = ∠ABF = $\frac{1}{2}$×(180° - 120°) = 30°, 同理, ∠EFD = 30°, ∴ ∠BFD = 120° - 30° - 30° = 60°. 如图, 过点 A 作 AG ⊥ BF 于点 G, 则 BG = FG,

在 Rt△AFG 中, ∵ ∠AFB = 30°, AF = 6, ∴ FG = $3\sqrt{3}$, ∴ BF = 2FG = $6\sqrt{3}$, 设圆锥的底面圆的半径为 r, 则 $2πr = \frac{60π×6\sqrt{3}}{180}$, ∴ $r = \sqrt{3}$.
答案 $\sqrt{3}$
解析 ∵ 多边形 ABCDEF 是正六边形, ∴ ∠BAF = ∠AFE = $\frac{(6 - 2)×180°}{6} = 120°$, AB = AF, ∴ ∠AFB = ∠ABF = $\frac{1}{2}$×(180° - 120°) = 30°, 同理, ∠EFD = 30°, ∴ ∠BFD = 120° - 30° - 30° = 60°. 如图, 过点 A 作 AG ⊥ BF 于点 G, 则 BG = FG,

在 Rt△AFG 中, ∵ ∠AFB = 30°, AF = 6, ∴ FG = $3\sqrt{3}$, ∴ BF = 2FG = $6\sqrt{3}$, 设圆锥的底面圆的半径为 r, 则 $2πr = \frac{60π×6\sqrt{3}}{180}$, ∴ $r = \sqrt{3}$.
9.「2024甘肃兰州中考」“轮动发石车”是我国古代的一种投石工具,在春秋战国时期被广泛应用,如图1所示的是陈列在展览馆的仿真模型.如图2所示的是模型驱动部分的示意图,其中$\odot M,\odot N$的半径分别是1 cm和10 cm,当$\odot M$顺时针转动3周时,$\odot N$上的点P随之旋转$n^{\circ }$,则$n=$
108
.答案:答案 108
解析 由题易知⊙M 的周长为 $2π$ cm, ∴ ⊙M 顺时针转动 3 周时, 点 P 移动的弧长为 $6π$ cm, ∴ $6π = \frac{nπ×10}{180}$, 解得 n = 108.
解析 由题易知⊙M 的周长为 $2π$ cm, ∴ ⊙M 顺时针转动 3 周时, 点 P 移动的弧长为 $6π$ cm, ∴ $6π = \frac{nπ×10}{180}$, 解得 n = 108.