1. (2023·福建)若某三角形的三边长分别为3,4,m,则m的值可以是 (
A. 1
B. 5
C. 7
D. 9
B
)A. 1
B. 5
C. 7
D. 9
答案:B
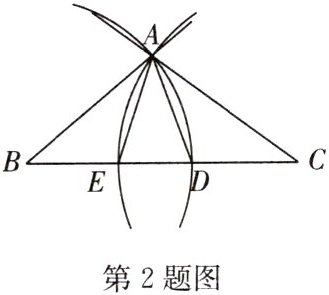
2. (2024春·宜兴期中)如图,已知△ABC,以点B为圆心,AB长为半径画弧,交BC于点D,以点C为圆心,AC长为半径画弧,交BC于点E.若∠B=40°,∠C=36°,则 (
A. AD=AE
B. AD<AE
C. BE=CD
D. BE<CD
D
)
A. AD=AE
B. AD<AE
C. BE=CD
D. BE<CD
答案:D
3. 一个三角形的两边长分别是2和7,最长边a为偶数,则这个三角形的周长为______
17
.答案:17
4. 已知一个三角形的三边长均为正整数,若其中仅有一条边长为5,且它又不是最短边,则满足条件的三角形有
10
个.答案:10
5. (2024秋·南京期中改编)在△ABC中,AC=3,BC=4.当AB=5时,△ABC是直角三角形;当△ABC是钝角三角形时,AB的长可能是______
6
.(写出一个符合要求的值)答案:6(答案不唯一)
6. (2024春·吴江区月考)已知a,b,c是一个三角形的三边长.
(1)若a=3,b=5,则c的取值范围是
(2)试化简:|b+c-a|+|b-c-a|+|c-a-b|.
解:∵b + c > a,a + c > b,a + b > c,
∴|b + c - a| + |b - c - a| + |c - a - b| = b + c - a + a + c - b + a + b - c =
(1)若a=3,b=5,则c的取值范围是
2<c<8
;(2)试化简:|b+c-a|+|b-c-a|+|c-a-b|.
解:∵b + c > a,a + c > b,a + b > c,
∴|b + c - a| + |b - c - a| + |c - a - b| = b + c - a + a + c - b + a + b - c =
a + b + c
.答案:(1)$2 < c < 8$
(2)解:$\because b + c > a,a + c > b,a + b > c,$
$\therefore |b + c - a| + |b - c - a| + |c - a - b| = b + c - a + a + c - b + a + b - c = a + b + c.$
(2)解:$\because b + c > a,a + c > b,a + b > c,$
$\therefore |b + c - a| + |b - c - a| + |c - a - b| = b + c - a + a + c - b + a + b - c = a + b + c.$
7. 在△ABC中,三边长分别为a,b,c,且满足a=b+2,b=c+1.
(1)试说明:b一定大于3;
解:因为$a = b + 2$,所以$b = a - 2,$
因为$b = c + 1$,所以$a - 2 = c + 1$,所以$a - c = 3.$
因为
(2)若这个三角形的周长为22,求a,b,c的值.
解:因为$b = c + 1$,所以$c = b - 1,$
所以
所以$a = b + 2 = $
(1)试说明:b一定大于3;
解:因为$a = b + 2$,所以$b = a - 2,$
因为$b = c + 1$,所以$a - 2 = c + 1$,所以$a - c = 3.$
因为
$a - c < b$
,所以$b$一定大于 3.(2)若这个三角形的周长为22,求a,b,c的值.
解:因为$b = c + 1$,所以$c = b - 1,$
所以
$b + 2 + b + b - 1 = 22$
,解得$b = 7$
.所以$a = b + 2 = $
9
,$c = b - 1 = $6
.答案:解:(1)因为$a = b + 2$,所以$b = a - 2,$
因为$b = c + 1$,所以$a - 2 = c + 1$,所以$a - c = 3.$
因为$a - c < b$,所以$b$一定大于 3.
(2)因为$b = c + 1$,所以$c = b - 1,$
所以$b + 2 + b + b - 1 = 22$,解得$b = 7.$
所以$a = b + 2 = 9,c = b - 1 = 6.$
因为$b = c + 1$,所以$a - 2 = c + 1$,所以$a - c = 3.$
因为$a - c < b$,所以$b$一定大于 3.
(2)因为$b = c + 1$,所以$c = b - 1,$
所以$b + 2 + b + b - 1 = 22$,解得$b = 7.$
所以$a = b + 2 = 9,c = b - 1 = 6.$