1.(2024·长沙)对于一次函数$y = 2x - 1$,下列结论正确的是 (
A.它的图象与$y$轴交于点$(0,-1)$
B.$y$随$x$的增大而减小
C.当$x>\frac {1}{2}$时,$y<0$
D.它的图象经过第一、二、三象限
A
)A.它的图象与$y$轴交于点$(0,-1)$
B.$y$随$x$的增大而减小
C.当$x>\frac {1}{2}$时,$y<0$
D.它的图象经过第一、二、三象限
答案:A
2.(2024 春·南通期末)若点$A(-2,y_{1}),B(3,y_{2}),C(1,y_{3})$在一次函数$y=-3x+m$($m$是常数)的图象上,则$y_{1},y_{2},y_{3}$的大小关系是 (
A.$y_{1}>y_{2}>y_{3}$
B.$y_{2}>y_{1}>y_{3}$
C.$y_{1}>y_{3}>y_{2}$
D.$y_{3}>y_{2}>y_{1}$
C
)A.$y_{1}>y_{2}>y_{3}$
B.$y_{2}>y_{1}>y_{3}$
C.$y_{1}>y_{3}>y_{2}$
D.$y_{3}>y_{2}>y_{1}$
答案:C
3.(2024·包头)在平面直角坐标系中,若一次函数的图象经过第一、二、三象限,请写出一个符合该条件的一次函数的表达式:
$y = x + 1$(答案不唯一)
.答案:$y = x + 1$(答案不唯一)
4.当$1≤x≤10$时,一次函数$y=-3x+b$的最大值为 18,则$b=$
21
.答案:21
5.已知关于$x$的函数$y=(2m - 2)x + m + 1$.
(1)当$m$为何值时,图象过原点?
(2)已知$y$随$x$的增大而增大,求$m$的取值范围;
(3)函数图象与$y$轴的交点在$x$轴上方,求$m$的取值范围;
(4)函数图象经过第一、二、四象限,求$m$的取值范围.
(1)当$m$为何值时,图象过原点?
(2)已知$y$随$x$的增大而增大,求$m$的取值范围;
(3)函数图象与$y$轴的交点在$x$轴上方,求$m$的取值范围;
(4)函数图象经过第一、二、四象限,求$m$的取值范围.
答案:解:(1) $ \because $ 函数图象过原点,
$ \therefore m + 1 = 0 $,即 $ m = -1 $。
(2) $ \because y $ 随 $ x $ 的增大而增大,
$ \therefore 2m - 2 > 0 $,解得 $ m > 1 $。
(3) $ \because $ 函数图象与 $ y $ 轴的交点在 $ x $ 轴上方,
$ \therefore m + 1 > 0 $,解得 $ m > -1 $。
(4) $ \because $ 函数图象经过第一、二、四象限,
$ \therefore \begin{cases} 2m - 2 < 0, \\ m + 1 > 0, \end{cases} \therefore -1 < m < 1 $。
$ \therefore m + 1 = 0 $,即 $ m = -1 $。
(2) $ \because y $ 随 $ x $ 的增大而增大,
$ \therefore 2m - 2 > 0 $,解得 $ m > 1 $。
(3) $ \because $ 函数图象与 $ y $ 轴的交点在 $ x $ 轴上方,
$ \therefore m + 1 > 0 $,解得 $ m > -1 $。
(4) $ \because $ 函数图象经过第一、二、四象限,
$ \therefore \begin{cases} 2m - 2 < 0, \\ m + 1 > 0, \end{cases} \therefore -1 < m < 1 $。
6.已知$A(x_{1},y_{1}),B(x_{2},y_{2})$是一次函数$y=kx - 3x + 2$的图象上的两个不同的点,若$(x_{1}-x_{2})(y_{1}-y_{2})<0$,则$k$的取值范围是 (
A.$k>3$
B.$k<3$
C.$k>2$
D.$k<2$
B
)A.$k>3$
B.$k<3$
C.$k>2$
D.$k<2$
答案:B
7.如图,在平面直角坐标系中,$\triangle ABC$的顶点坐标分别是$A(1,1),B(3,1),C(2,2)$,当直线$y=\frac {1}{2}x + b$与$\triangle ABC$有交点时,$b$的取值范围是 (
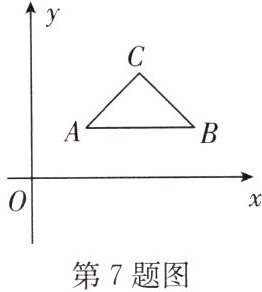
A.$-1≤b≤1$
B.$-\frac {1}{2}≤b≤1$
C.$-\frac {1}{2}≤b≤\frac {1}{2}$
D.$-1≤b≤\frac {1}{2}$
B
)
A.$-1≤b≤1$
B.$-\frac {1}{2}≤b≤1$
C.$-\frac {1}{2}≤b≤\frac {1}{2}$
D.$-1≤b≤\frac {1}{2}$
答案:B
8.(2024 春·玄武区月考)已知过点$(1,3)$的直线$y = ax + b(a≠0)$不经过第四象限,设$S = a + 2b$,则$S$的取值范围为
$3 \leq S < 6$
.答案:$3 \leq S < 6 $