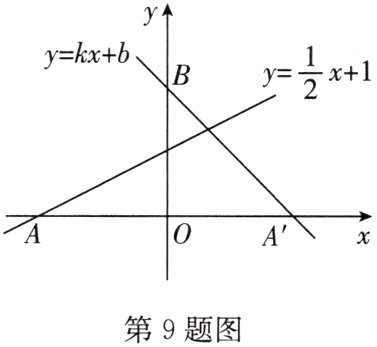
9.(10分)如图,直线$y=\frac {1}{2}x+1$与x轴交于点A,点A关于y轴的对称点为$A'$,点$B(0,2)$,设直线$A'B$的函数表达式为$y=kx+b$.
(1)求点$A'$的坐标;
(2)确定直线$A'B$对应的函数表达式.
(1)求点$A'$的坐标;
(2, 0)
(2)确定直线$A'B$对应的函数表达式.
$y = - x + 2$

答案:解: (1) 令 $y = 0$, 则 $ \frac { 1 } { 2 } x + 1 = 0 $, $ \therefore x = - 2 $, $ \therefore A ( - 2, 0 ) $.
∵ 点 $A$ 关于 $y$ 轴的对称点为 $A ^ { \prime }$, $ \therefore A ^ { \prime } ( 2, 0 ) $.
(2) 将 $ ( 2, 0 ) $, $ ( 0, 2 ) $ 代入 $y = k x + b$, 得
$ \left\{ \begin{array} { l } { 2 k + b = 0, } \\ { b = 2, } \end{array} \right. $ 解得 $ \left\{ \begin{array} { l } { k = - 1, } \\ { b = 2, } \end{array} \right. $
∴ 直线 $A ^ { \prime }B$ 对应的函数表达式为 $y = - x + 2$.
∵ 点 $A$ 关于 $y$ 轴的对称点为 $A ^ { \prime }$, $ \therefore A ^ { \prime } ( 2, 0 ) $.
(2) 将 $ ( 2, 0 ) $, $ ( 0, 2 ) $ 代入 $y = k x + b$, 得
$ \left\{ \begin{array} { l } { 2 k + b = 0, } \\ { b = 2, } \end{array} \right. $ 解得 $ \left\{ \begin{array} { l } { k = - 1, } \\ { b = 2, } \end{array} \right. $
∴ 直线 $A ^ { \prime }B$ 对应的函数表达式为 $y = - x + 2$.
10.(10分)(2024·包头)如图是1个碗和4个整齐叠放成一摞的碗的示意图,碗的规格都是相同的.小亮尝试结合学习函数的经验,探究整齐叠放成一摞的这种规格的碗的总高度y(单位:cm)随着碗的数量x(单位:个)的变化规律.下表是小亮经过测量得到的y与x之间的对应数据:
|x/个|1|2|3|4|
|----|----|----|----|----|
|y/cm|6|8.4|10.8|13.2|
(1)依据小亮测量的数据,写出y与x之间的函数表达式,并说明理由;
(2)若整齐叠放成一摞的这种规格的碗的总高度不超过28.8 cm,此时碗的数量最多为多少个?
|x/个|1|2|3|4|
|----|----|----|----|----|
|y/cm|6|8.4|10.8|13.2|
(1)依据小亮测量的数据,写出y与x之间的函数表达式,并说明理由;
y = 2.4 x + 3.6
(2)若整齐叠放成一摞的这种规格的碗的总高度不超过28.8 cm,此时碗的数量最多为多少个?
10
答案:解: (1) 由表中的数据知 $y$ 是 $x$ 的一次函数, 设 $y = k x + b$,
由题意得 $ \left\{ \begin{array} { l } { k + b = 6, } \\ { 2 k + b = 8.4, } \end{array} \right. $ 解得 $ \left\{ \begin{array} { l } { k = 2.4, } \\ { b = 3.6, } \end{array} \right. $
∴ $y$ 与 $x$ 之间的函数表达式为 $y = 2.4 x + 3.6$.
(2) 设碗的数量为 $x$ 个, 则 $2.4 x + 3.6 \leq 28.8$,
解得 $x \leq 10.5$,
∴ $x$ 的最大整数解为 10.
答: 此时碗的数量最多为 10 个.
由题意得 $ \left\{ \begin{array} { l } { k + b = 6, } \\ { 2 k + b = 8.4, } \end{array} \right. $ 解得 $ \left\{ \begin{array} { l } { k = 2.4, } \\ { b = 3.6, } \end{array} \right. $
∴ $y$ 与 $x$ 之间的函数表达式为 $y = 2.4 x + 3.6$.
(2) 设碗的数量为 $x$ 个, 则 $2.4 x + 3.6 \leq 28.8$,
解得 $x \leq 10.5$,
∴ $x$ 的最大整数解为 10.
答: 此时碗的数量最多为 10 个.
11.(10分)(2024·苏州期末)如图,直线$y=x+3$与y轴交于点A,点B为该直线上一点,且点B的纵坐标是6.
(1)求点A和点B的坐标;
(2)把直线$y=x+3$向下平移7个单位长度,若平移后的直线与x轴交于点C,连接AC,BC,求$\triangle ABC$的面积.

(1)求点A和点B的坐标;
(2)把直线$y=x+3$向下平移7个单位长度,若平移后的直线与x轴交于点C,连接AC,BC,求$\triangle ABC$的面积.

答案:
解: (1) 把 $x = 0$ 代入 $y = x + 3$, 得 $y = 3$, $ \therefore A ( 0, 3 ) $.
把 $y = 6$ 代入 $y = x + 3$, 得 $6 = x + 3$, 解得 $x = 3$,
∴ $B ( 3, 6 ) $.
(2) 如答图, 设直线 $AB$ 与 $x$ 轴交于点 $E$.

在 $y = x + 3$ 中, 令 $y = 0$ 得 $x = - 3$, $ \therefore E ( - 3, 0 ) $,
把直线 $y = x + 3$ 向下平移 7 个单位长度得到直线: $y = x + 3 - 7$, 即 $y = x - 4$,
在 $y = x - 4$ 中, 令 $y = 0$ 得 $x - 4 = 0$, 解得 $x = 4$,
∴ $C ( 4, 0 ) $, $ \therefore C E = 7 $,
$ \therefore S _ { \triangle A B C } = S _ { \triangle B C E } - S _ { \triangle A C E } = \frac { 1 } { 2 } C E \cdot y _ { B } - \frac { 1 } { 2 } C E \cdot y _ { A } = \frac { 1 } { 2 } C E \cdot ( y _ { B } - y _ { A } ) = \frac { 1 } { 2 } \times 7 \times ( 6 - 3 ) = \frac { 21 } { 2 } $.
∴ $ \triangle A B C $ 的面积为 $ \frac { 21 } { 2 } $.
解: (1) 把 $x = 0$ 代入 $y = x + 3$, 得 $y = 3$, $ \therefore A ( 0, 3 ) $.
把 $y = 6$ 代入 $y = x + 3$, 得 $6 = x + 3$, 解得 $x = 3$,
∴ $B ( 3, 6 ) $.
(2) 如答图, 设直线 $AB$ 与 $x$ 轴交于点 $E$.

在 $y = x + 3$ 中, 令 $y = 0$ 得 $x = - 3$, $ \therefore E ( - 3, 0 ) $,
把直线 $y = x + 3$ 向下平移 7 个单位长度得到直线: $y = x + 3 - 7$, 即 $y = x - 4$,
在 $y = x - 4$ 中, 令 $y = 0$ 得 $x - 4 = 0$, 解得 $x = 4$,
∴ $C ( 4, 0 ) $, $ \therefore C E = 7 $,
$ \therefore S _ { \triangle A B C } = S _ { \triangle B C E } - S _ { \triangle A C E } = \frac { 1 } { 2 } C E \cdot y _ { B } - \frac { 1 } { 2 } C E \cdot y _ { A } = \frac { 1 } { 2 } C E \cdot ( y _ { B } - y _ { A } ) = \frac { 1 } { 2 } \times 7 \times ( 6 - 3 ) = \frac { 21 } { 2 } $.
∴ $ \triangle A B C $ 的面积为 $ \frac { 21 } { 2 } $.