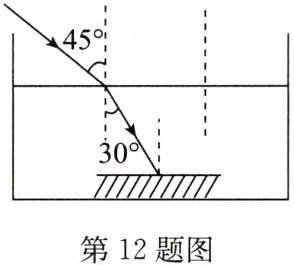
12. (2024·武进区校级一模)如图所示,光线从空气射入某种液体中,入射角为$45^{\circ }$,折射角为$30^{\circ }$,光线射到液体底部水平放置的平面镜上又反射回来,最后光线又回到空气中的折射角是 (
A.$30^{\circ }$
B.$45^{\circ }$
C.$55^{\circ }$
D.$60^{\circ }$
B
)
A.$30^{\circ }$
B.$45^{\circ }$
C.$55^{\circ }$
D.$60^{\circ }$
答案:B
解析:
解:光线从空气射入液体时,入射角$i_1 = 45^\circ$,折射角$r_1 = 30^\circ$。根据光的折射定律,液体对空气的折射率$n=\frac{\sin i_1}{\sin r_1}=\frac{\sin 45^\circ}{\sin 30^\circ}=\frac{\frac{\sqrt{2}}{2}}{\frac{1}{2}}=\sqrt{2}$。
光线射到平面镜上反射,反射角等于入射角,此时入射角为$30^\circ$,故反射角也为$30^\circ$,反射光线与法线夹角为$30^\circ$,即反射光线在液体中射向空气时的入射角$i_2 = 30^\circ$。
光线从液体射回空气,根据折射定律$\frac{\sin r_2}{\sin i_2}=\frac{1}{n}$,则$\sin r_2 = \frac{\sin i_2}{n}=\frac{\sin 30^\circ}{\sqrt{2}}=\frac{\frac{1}{2}}{\sqrt{2}}=\frac{\sqrt{2}}{4}$(此步计算仅为推导,实际根据光路可逆性,此时折射角$r_2 = i_1 = 45^\circ$)。
最终光线回到空气中的折射角是$45^\circ$。
答案:B
光线射到平面镜上反射,反射角等于入射角,此时入射角为$30^\circ$,故反射角也为$30^\circ$,反射光线与法线夹角为$30^\circ$,即反射光线在液体中射向空气时的入射角$i_2 = 30^\circ$。
光线从液体射回空气,根据折射定律$\frac{\sin r_2}{\sin i_2}=\frac{1}{n}$,则$\sin r_2 = \frac{\sin i_2}{n}=\frac{\sin 30^\circ}{\sqrt{2}}=\frac{\frac{1}{2}}{\sqrt{2}}=\frac{\sqrt{2}}{4}$(此步计算仅为推导,实际根据光路可逆性,此时折射角$r_2 = i_1 = 45^\circ$)。
最终光线回到空气中的折射角是$45^\circ$。
答案:B
13. 学校新建成一个喷水池,在池底的中央安装一只射灯.经过连续几天观察,小敏同学发现:池内无水时,射灯发出的一束光照在池壁上,在 S 点形成一个亮斑,如图所示;当池内水面升至 a 位置时,她在池旁看到亮斑的位置在 P 点;当水面升至 b 位置时,她看到亮斑的位置在 Q 点.则 (

A.P 点在 S 点的上方
B.Q 点在 S 点的上方
C.P 点和 S 点重合
D.Q 点和 S 点重合
B
)
A.P 点在 S 点的上方
B.Q 点在 S 点的上方
C.P 点和 S 点重合
D.Q 点和 S 点重合
答案:B
解析:
解:池内无水时,光沿直线传播,亮斑在S点。
当水面升至a位置时,光从水斜射入空气,折射角大于入射角,人眼逆着折射光线看到的P点在S点下方。
当水面升至b位置时,光在水中沿直线传播到S点正下方池壁,再折射入空气,人眼看到的Q点在S点上方。
结论:Q点在S点的上方。
答案:B
当水面升至a位置时,光从水斜射入空气,折射角大于入射角,人眼逆着折射光线看到的P点在S点下方。
当水面升至b位置时,光在水中沿直线传播到S点正下方池壁,再折射入空气,人眼看到的Q点在S点上方。
结论:Q点在S点的上方。
答案:B
14. 如图所示,某同学从 A 处向水中看去,看到刻度尺上水中 B 点所成的像位于 C 点,请完成该同学从 A 处看到 B 点的光路图(虚线为水面位置).


答案:
如答图所示

如答图所示

15. 如图是小明眼睛在 N 点看到鱼缸内 M 点处鹅卵石的光路图.鱼缸内注入更多水后,小明的眼睛在 N 点仍然可以看到鹅卵石.选项中带箭头的虚线代表原来的光路,能正确反映水变多后小明看到鹅卵石的光路图是 (


C
)

答案:C
解析:
解:当鱼缸内注入更多水后,水面升高,鹅卵石M点的位置不变,但入射点会向右移动。光从水中斜射入空气中时,折射角大于入射角,且折射光线的反向延长线过像点。原来的光路中,入射点在较低位置,水增多后,入射点上移且右移,折射光线仍要进入眼睛N点,对比各选项,只有C选项符合上述光路变化规律。
答案:C
答案:C