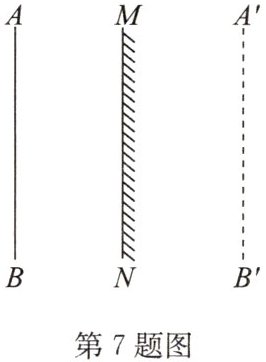
7. 小明身高 $1.8$ 米(图中用 $AB$ 表示),他想要在家里竖直墙上安装一面穿衣镜。爸爸告诉他,想通过平面镜看自己的全身像,平面镜长度最小只要身高的一半就够了,请你帮助小明完成下列任务。
(1) 分别画出 $A$ 点的光线通过平面镜反射进入眼睛的光路和 $B$ 点的光线通过平面镜反射进入眼睛的光路(假设眼睛在 $A$ 点)。
(2) 推导分析通过平面镜看自己的全身像,平面镜最小的长度值。
(1) 分别画出 $A$ 点的光线通过平面镜反射进入眼睛的光路和 $B$ 点的光线通过平面镜反射进入眼睛的光路(假设眼睛在 $A$ 点)。
(2) 推导分析通过平面镜看自己的全身像,平面镜最小的长度值。

答案:
(1)A点的光线垂直射向平面镜,反射光线沿原路返回进入眼睛,先作出B关于平面镜的对称点B',即B在平面镜中成的像,连接B'和人的眼睛A,与平面镜交于O,连接BO就是入射光线,OA为反射光线,即为B点的光线通过平面镜反射进入眼睛的光路,如答图所示.
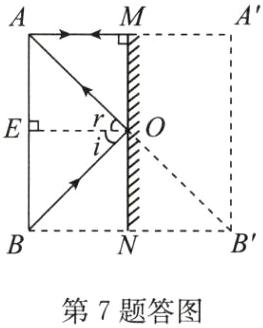
(2)由答图可知,平面镜的上端与人的眼睛等高,B点是人的脚,A点是人的眼睛.从脚上反射出来的光线到达镜子的最下端,经过平面镜的反射刚好进入人的眼睛.
因为∠r=∠i(反射定律),
OE为公共边,∠AEO=∠BEO=90°,
所以△AEO≌△BEO(角、边、角),
AE=BE=OM=$\frac{1}{2}$×AB=$\frac{1}{2}$×1.8m=0.9m.
故小明想通过平面镜看自己的全身像,则平面镜的高度至少为整个身高的一半,为0.9m.
(1)A点的光线垂直射向平面镜,反射光线沿原路返回进入眼睛,先作出B关于平面镜的对称点B',即B在平面镜中成的像,连接B'和人的眼睛A,与平面镜交于O,连接BO就是入射光线,OA为反射光线,即为B点的光线通过平面镜反射进入眼睛的光路,如答图所示.

(2)由答图可知,平面镜的上端与人的眼睛等高,B点是人的脚,A点是人的眼睛.从脚上反射出来的光线到达镜子的最下端,经过平面镜的反射刚好进入人的眼睛.
因为∠r=∠i(反射定律),
OE为公共边,∠AEO=∠BEO=90°,
所以△AEO≌△BEO(角、边、角),
AE=BE=OM=$\frac{1}{2}$×AB=$\frac{1}{2}$×1.8m=0.9m.
故小明想通过平面镜看自己的全身像,则平面镜的高度至少为整个身高的一半,为0.9m.
8. 如图,$A$、$B$ 两地相距 $4\mathrm{km}$,$MN$ 是与 $AB$ 连线平行的一条小河的河岸,$AB$ 到河岸的垂直距离为 $3\mathrm{km}$,小军要从 $A$ 处走到河岸取水然后送到 $B$ 处,他先沿着垂直于河岸的方向到 $D$ 点取水,再沿直线 $DB$ 到 $B$。若小军的速度大小恒为 $5\mathrm{km/h}$,不考虑取水停留的时间。
(1) 求小军完成这次取水和送水任务所需的时间。
(2) 为了找到一条最短路线(即从 $A$ 到河岸和从河岸到 $B$ 的总路程最短),可以将 $MN$ 看成一个平面镜,从 $A$ 点作出一条光线经 $MN$ 反射后恰能通过 $B$ 点,请你证明入射点 $O$ 即为最短路线的取水点。

(1) 求小军完成这次取水和送水任务所需的时间。
(2) 为了找到一条最短路线(即从 $A$ 到河岸和从河岸到 $B$ 的总路程最短),可以将 $MN$ 看成一个平面镜,从 $A$ 点作出一条光线经 $MN$ 反射后恰能通过 $B$ 点,请你证明入射点 $O$ 即为最短路线的取水点。

答案:
$(1)$如答图甲所示,小军通过的路程是$s_{AD}+s_{DB},$
此时,$s_{AB}=4km,$$s_{AD}=3km,$根据勾股定理可知,$s_{DB}=5km,$

故小军通过的路程$s=s_{AD}+s_{DB}=3km+5km=8km,$
∵$v=\frac{s}{t},$∴所需的时间$t=\frac{s}{v}=\frac{8km}{5km/h}=1.6h.$
$(2)$作出点$A$关于平面镜的对称点,即为像点$A',$连接$A'、$$B$交平面镜于点$O,$沿$OB$画出反射光线,连接$AO$画出入射光线,如答图乙所示,图中$O$就是入射点$.$

$①$由答图可知,$A'B$的连线是线段,两点之间,线段最短,即此时$A'B$之间的距离$(s_{A'O}+s_{OB})$最短$.$
$②$根据平面镜成像的特点可知,此时$s_{AD}=s_{A'D},$且$Rt△ADO$与$Rt△A'DO$有一条公共边$DO,$故可知$Rt△ADO≌Rt△A'DO,$即$s_{AO}=s_{A'O};$
故$s_{AO}+s_{OB}=s_{A'O}+s_{OB};$
即此时$O$点是最短路线的取水点$.$
$(1)$如答图甲所示,小军通过的路程是$s_{AD}+s_{DB},$
此时,$s_{AB}=4km,$$s_{AD}=3km,$根据勾股定理可知,$s_{DB}=5km,$

故小军通过的路程$s=s_{AD}+s_{DB}=3km+5km=8km,$
∵$v=\frac{s}{t},$∴所需的时间$t=\frac{s}{v}=\frac{8km}{5km/h}=1.6h.$
$(2)$作出点$A$关于平面镜的对称点,即为像点$A',$连接$A'、$$B$交平面镜于点$O,$沿$OB$画出反射光线,连接$AO$画出入射光线,如答图乙所示,图中$O$就是入射点$.$

$①$由答图可知,$A'B$的连线是线段,两点之间,线段最短,即此时$A'B$之间的距离$(s_{A'O}+s_{OB})$最短$.$
$②$根据平面镜成像的特点可知,此时$s_{AD}=s_{A'D},$且$Rt△ADO$与$Rt△A'DO$有一条公共边$DO,$故可知$Rt△ADO≌Rt△A'DO,$即$s_{AO}=s_{A'O};$
故$s_{AO}+s_{OB}=s_{A'O}+s_{OB};$
即此时$O$点是最短路线的取水点$.$