1. 两支内径不同、玻璃泡内水银量相等的合格温度计,同时插入一杯热水中,经过一段时间后,会看到(
A.两支温度计水银柱上升的高度相同,示数相同
B.内径细的温度计水银柱上升得较高,示数较大
C.内径粗的温度计水银柱上升得较高,示数较大
D.内径粗的温度计水银柱上升得较低,两支温度计的示数相同
D
)A.两支温度计水银柱上升的高度相同,示数相同
B.内径细的温度计水银柱上升得较高,示数较大
C.内径粗的温度计水银柱上升得较高,示数较大
D.内径粗的温度计水银柱上升得较低,两支温度计的示数相同
答案:D
解析:
解:合格温度计示数由热水温度决定,故两支温度计示数相同。玻璃泡内水银量相等,受热后膨胀体积相同,内径粗的横截面积大,根据$h = \frac{V}{S}$($V$为膨胀体积,$S$为横截面积),内径粗的水银柱上升高度较低。
结论:D
结论:D
2. 用两支体温计给两位病人测量体温,读数都是$37.5^{\circ}C$。若在不甩的情况下,直接给另外两位病人测量体温(这两位病人的实际体温分别是$36.5^{\circ}C和39.5^{\circ}C$),则这两支体温计的读数将分别为(
A.$37.5^{\circ}C$、$39.5^{\circ}C$
B.都是$37.5^{\circ}C$
C.都是$39.5^{\circ}C$
D.$36.5^{\circ}C$、$39.5^{\circ}C$
A
)A.$37.5^{\circ}C$、$39.5^{\circ}C$
B.都是$37.5^{\circ}C$
C.都是$39.5^{\circ}C$
D.$36.5^{\circ}C$、$39.5^{\circ}C$
答案:A
解析:
体温计的特殊构造使得其示数只能上升不能下降(在不甩的情况下)。
第一支体温计初始读数为$37.5^{\circ}C$,测量实际体温$36.5^{\circ}C$的病人时,因$36.5^{\circ}C<37.5^{\circ}C$,示数不变,仍为$37.5^{\circ}C$;
第二支体温计初始读数为$37.5^{\circ}C$,测量实际体温$39.5^{\circ}C$的病人时,因$39.5^{\circ}C>37.5^{\circ}C$,示数上升至$39.5^{\circ}C$。
答案:A
第一支体温计初始读数为$37.5^{\circ}C$,测量实际体温$36.5^{\circ}C$的病人时,因$36.5^{\circ}C<37.5^{\circ}C$,示数不变,仍为$37.5^{\circ}C$;
第二支体温计初始读数为$37.5^{\circ}C$,测量实际体温$39.5^{\circ}C$的病人时,因$39.5^{\circ}C>37.5^{\circ}C$,示数上升至$39.5^{\circ}C$。
答案:A
3. 在如图温度计所示的恒温环境下进行实验。将温度计放入一杯冰水混合物中(冰是晶体),从温度计放入开始计时,放入时间足够长,下列哪幅示意图可能反映了温度计内液体的体积随时间变化的情况(
A
)答案:A
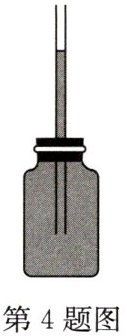
4. 利用玻璃瓶、玻璃管、橡皮塞、适量带颜色的水可以自制温度计(如图所示),为了提高自制温度计的精确度,下列方法可行的是(
①使用更粗的玻璃管 ②使用更细的玻璃管 ③换用更大的玻璃瓶装水 ④换用更小的玻璃瓶装水
A.①③
B.②③
C.②④
D.①④
B
)①使用更粗的玻璃管 ②使用更细的玻璃管 ③换用更大的玻璃瓶装水 ④换用更小的玻璃瓶装水

A.①③
B.②③
C.②④
D.①④
答案:B
解析:
解:自制温度计是利用液体热胀冷缩的性质工作的。
玻璃管越细,相同体积变化时液柱高度变化越明显,精确度越高,故②可行,①不可行;
玻璃瓶越大,瓶内液体越多,温度变化时液体体积变化越大,液柱高度变化越明显,精确度越高,故③可行,④不可行。
综上,可行的方法是②③,答案选B。
玻璃管越细,相同体积变化时液柱高度变化越明显,精确度越高,故②可行,①不可行;
玻璃瓶越大,瓶内液体越多,温度变化时液体体积变化越大,液柱高度变化越明显,精确度越高,故③可行,④不可行。
综上,可行的方法是②③,答案选B。
5. 一个标准大气压下,将一支刻度均匀的温度计放在冰水混合物中时,示数为$10^{\circ}C$;用它测沸水的温度时,示数是$90^{\circ}C$。若用它测得某容器中温水的温度为$70^{\circ}C$,则温水的实际温度应为(
A.$56^{\circ}C$
B.$60^{\circ}C$
C.$75^{\circ}C$
D.$80^{\circ}C$
C
)A.$56^{\circ}C$
B.$60^{\circ}C$
C.$75^{\circ}C$
D.$80^{\circ}C$
答案:C 点拨:在温度的定义中,规定在一个标准大气压下冰水混合物的温度为 $ 0^{\circ}C $,水沸腾时的温度为 $ 100^{\circ}C $。然后将 $ 0^{\circ}C $ 到 $ 100^{\circ}C $ 平均分为 100 份,每份是 $ 1^{\circ}C $。本题中,按照温度的定义,题中的温度计 $ 1^{\circ}C $ 对应的标准温度计的度数为 $ 100^{\circ}C ÷ (90 - 10) = 1.25^{\circ}C $。当测得的温水的温度为 $ 70^{\circ}C $ 时,实际温度为 $ 1.25^{\circ}C × (70 - 10) = 75^{\circ}C $。