1. 先说一说商是几位数,再用竖式计算。
$97÷30$
$97÷30$
$3\cdots\cdots7$
$209÷20$$10\cdots\cdots9$
答案:说一说略 $3\cdots\cdots7$ $10\cdots\cdots9$ 竖式略
2. (1) 要使$□36÷30$的商是一位数,
□里可以填(
□0的商是两位数,□里可以
填(
□里可以填(
1,2
);要使$523÷$□0的商是两位数,□里可以
填(
1,2,3,4,5
)。答案:(1) 1,2 1,2,3,4,5
(2) 一个数除以30,商是12,有余数,这个数最大是
389
,最小是361
。答案:(2) 389 361
解析:
解:
因为余数小于除数,除数是30,所以余数最大为29,最小为1。
当余数最大时,这个数最大:$30×12 + 29 = 360 + 29 = 389$
当余数最小时,这个数最小:$30×12 + 1 = 360 + 1 = 361$
389;361
因为余数小于除数,除数是30,所以余数最大为29,最小为1。
当余数最大时,这个数最大:$30×12 + 29 = 360 + 29 = 389$
当余数最小时,这个数最小:$30×12 + 1 = 360 + 1 = 361$
389;361
|每辆车装的箱数|10|20|30|40|60|
|要装几车|
发现:
80
||要装几车|
48
|24
|16
|12
|8
|6|发现:
总箱数不变,每辆车装的箱数越多,要装的车数就越少
。答案:(3) 48 24 16 12 8 80 总箱数不变,每辆车装的箱数越多,要装的车数就越少
解析:
|每辆车装的箱数|10|20|30|40|60|80|
|----|----|----|----|----|----|----|
|要装几车|48|24|16|12|8|6|
发现:总箱数不变,每辆车装的箱数越多,要装的车数就越少。
|----|----|----|----|----|----|----|
|要装几车|48|24|16|12|8|6|
发现:总箱数不变,每辆车装的箱数越多,要装的车数就越少。
3. 位于西安的秦始皇陵兵马俑被誉为“世界第八大奇迹”。四年级有316名师生去参观,旅游公司有两种型号的客车(如图)。若只能从中租一种型号的车,且要使空的座位最少,则应怎样租车?(不考虑驾驶座)
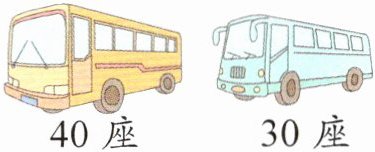

答案:$316÷40 = 7$(辆)$\cdots\cdots36$(人) $40 - 36 = 4$(个)$316÷30 = 10$(辆)$\cdots\cdots16$(人) $30 - 16 = 14$(个)$4\lt14$ $7 + 1 = 8$(辆) 要使空的座位最少,应租 $8$ 辆 $40$ 座的车。
解析:
解:
$316÷40=7$(辆)$\cdots\cdots36$(人)
$7+1=8$(辆)
空座位数:$40×8-316=4$(个)
$316÷30=10$(辆)$\cdots\cdots16$(人)
$10+1=11$(辆)
空座位数:$30×11-316=14$(个)
$4\lt14$
应租8辆40座的车。
$316÷40=7$(辆)$\cdots\cdots36$(人)
$7+1=8$(辆)
空座位数:$40×8-316=4$(个)
$316÷30=10$(辆)$\cdots\cdots16$(人)
$10+1=11$(辆)
空座位数:$30×11-316=14$(个)
$4\lt14$
应租8辆40座的车。
4. 在一道有余数的除法算式中,被除数与除数的和是144。若商是19,余数是4,则被除数是(
137
),除数是(7
)。答案:137 7
解析:
解:设除数是$x$,则被除数是$19x + 4$。
由题意得:$19x + 4 + x = 144$
$20x + 4 = 144$
$20x = 140$
$x = 7$
被除数:$19×7 + 4 = 137$
137;7
由题意得:$19x + 4 + x = 144$
$20x + 4 = 144$
$20x = 140$
$x = 7$
被除数:$19×7 + 4 = 137$
137;7
5. (2025·连云港灌云县期末)王娟读一本241页的书,她今天读完的最后两页页码之和是121,如果她接下来按每天读30页,还需要多少天才能读完?
答案:$(121 - 1)÷2 = 60$(页) $60 + 1 = 61$(页)$(241 - 61)÷30 = 6$(天)
6. $□8□÷40$的余数是24,被除数有(
5
)种不同的可能。答案:5 解析 余数是 $24$,除数是 $40$,那么被除数的个位只能是 $4$。可通过计算得出算式分别为① $184÷40 = 4\cdots\cdots24$;② $384÷40 = 9\cdots\cdots24$;③ $584÷40 = 14\cdots\cdots24$;④ $784÷40 = 19\cdots\cdots24$;⑤ $984÷40 = 24\cdots\cdots24$。
解析:
解:因为余数是24,除数是40,所以被除数的个位数字为4。设被除数为$a84$($a$为百位上的数字,$a$为1 - 9的整数)。
根据被除数 = 商×除数 + 余数,可得$a84 = 40×商 + 24$,即$a84 - 24 = 40×商$,$a60 = 40×商$,$商 = a60÷40 = (10a + 6)÷4$。
商为整数,则$10a + 6$能被4整除:
当$a = 1$时,$10×1 + 6 = 16$,$16÷4 = 4$,商为4,被除数184;
当$a = 3$时,$10×3 + 6 = 36$,$36÷4 = 9$,商为9,被除数384;
当$a = 5$时,$10×5 + 6 = 56$,$56÷4 = 14$,商为14,被除数584;
当$a = 7$时,$10×7 + 6 = 76$,$76÷4 = 19$,商为19,被除数784;
当$a = 9$时,$10×9 + 6 = 96$,$96÷4 = 24$,商为24,被除数984。
共5种不同可能。
答案:5
根据被除数 = 商×除数 + 余数,可得$a84 = 40×商 + 24$,即$a84 - 24 = 40×商$,$a60 = 40×商$,$商 = a60÷40 = (10a + 6)÷4$。
商为整数,则$10a + 6$能被4整除:
当$a = 1$时,$10×1 + 6 = 16$,$16÷4 = 4$,商为4,被除数184;
当$a = 3$时,$10×3 + 6 = 36$,$36÷4 = 9$,商为9,被除数384;
当$a = 5$时,$10×5 + 6 = 56$,$56÷4 = 14$,商为14,被除数584;
当$a = 7$时,$10×7 + 6 = 76$,$76÷4 = 19$,商为19,被除数784;
当$a = 9$时,$10×9 + 6 = 96$,$96÷4 = 24$,商为24,被除数984。
共5种不同可能。
答案:5
7. 亮点原创·“果中甘露子,药中圣醍醐”,砀山酥梨酥脆爽口,润肺止咳,是中国传统三大名梨之首。张叔叔的水果店采购了24箱相同质量的砀山酥梨。若从每箱中取出15千克,则这24箱中剩下的梨的质量与原来4箱中梨的质量相同。现在每箱中有多少千克梨?
答案:$24×15 = 360$(千克) $24 - 4 = 20$(箱)$360÷20 = 18$(千克) $18 - 15 = 3$(千克)解析 根据“这 $24$ 箱中剩下的梨的质量与原来 $4$ 箱中梨的质量相同”可知,取出的 $24×15 = 360$(千克)是原来 $24 - 4 = 20$(箱)梨的质量,则原来每箱中有 $360÷20 = 18$(千克)梨,所以现在每箱中有 $18 - 15 = 3$(千克)梨。
解析:
解:24×15=360(千克)
24-4=20(箱)
360÷20=18(千克)
18-15=3(千克)
答:现在每箱中有3千克梨。
24-4=20(箱)
360÷20=18(千克)
18-15=3(千克)
答:现在每箱中有3千克梨。