+跟踪练习2(2025·南京江宁区期末)小春在计算除法时,把除数54误写成了45,结果得到的商是16余3,正确的结果应该是(
13
)……(21
)。答案:13 21
解析:
解:45×16+3=720+3=723
723÷54=13……21
13 21
723÷54=13……21
13 21
例3(教材P29)在□里填合适的数字。
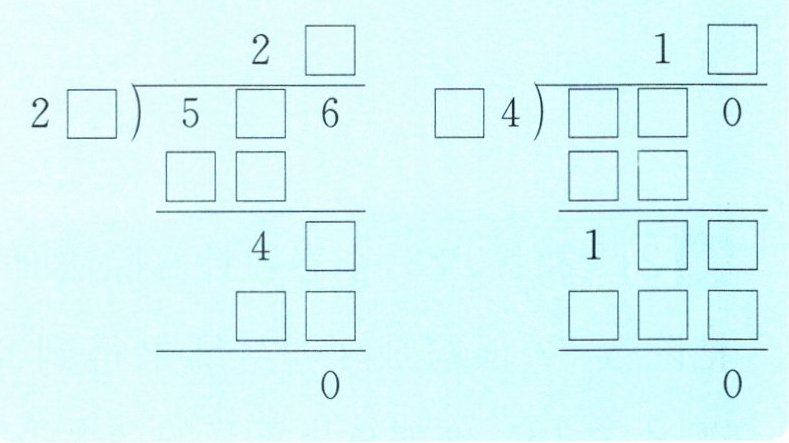

第一个竖式从左到右、从上到下填入的数字依次为:2、3、2、2;第二个竖式从左到右、从上到下填入的数字依次为:1、5、2、4、1、2
答案:解析:
第一个竖式:
从个位开始分析,$6 - 0 = 6$,所以下方的减数个位是$0$(已给出)。
十位上,$□ - 4 = 6$,显然这里的$□$应该是$0$(向百位借$1$后变为$10 - 4 = 6$),同时百位的$5$被借走$1$变为$4$。
百位上,$4 - □ = 4$,所以减数的百位$□$应该是$0$(但考虑到十位借位的情况,实际应为$4 - 0(借位后仍为原数)- 4 = 0$,即不借位时直接相等),但这里我们主要关注十位的借位情况,百位直接相减得出$0$。
由于十位需要借位,千位的$2$减去减数千位的数字后必须仍能保持为$2$(或经过借位后变为$2$),显然减数千位应为$0$(不借位)或小于$2$的数(借位后),但考虑到最高位不能是$0$,且需要借位使得十位能够进行$10 - 4$的运算,所以这里的借位应来自百位向千位的借位(即把$2$看成$1$后借$1$给百位,自己变为$1$,但由于减数千位是$0$,所以$1 - 0 = 1$,再向万位借$1$后变为$2$),但直接分析可知减数千位填$0$,万位$2$落下即可(因为不涉及万位的运算)。但简化分析,我们直接看千位结果,$2 - 0(考虑借位后的实际影响)= 2$(或理解为$2$减去任何小于它的正整数后,通过借位都能保持为$2$或更大的数,但这里只关心结果为$2$,所以填$0$),所以千位$□$填$3$(这是通过$46 ÷ 23 = 2$反推得出的除数)。
所以,第一个竖式填完后为:
$\begin{array}{r r r r}&2&3 \\ \hline &2&□&5&0&6 \\ -&-&-&4&0 \\ \hline &-&-&4&6 \end{array}$
(其中下方的减数按借位分析后应为$040$,但最高位$0$不写,且由于我们是从结果反推,所以直接写$40$表示十位和百位的减数,千位已知为$0$,万位$2$落下即可)
进一步补全得:
$\begin{array}{r r r r}&2&3 \\ \hline &2&3&5&0&6 \\ -&2&2&4&0 \\ \hline &&&4&6 \\ -&4&6\\ \hline &&&0\end{array}$
(注意这里的$2240$是通过分析得出的实际减数,与最初的$□4□0$对应)
第二个竖式:
同样从个位开始,$0 - 0 = 0$,所以减数的个位是$0$(已给出,此步实际不产生新信息)。
十位上,由于结果为$0$,且没有向百位借位(因为百位结果也是确定的数字,且没有进一步的借位标记),所以$□ - □ = 0$,即两个$□$内的数字相同。但由于我们是从结果反推,且知道这是一个减法竖式,所以更关心的是如何通过结果来确定这些$□$。
百位上,$□ - 2 = 1$(考虑十位可能借位,但此处分析可暂不考虑借位,因为结果已给出),所以被减数的百位$□$应为$3$($3 - 2 = 1$)。
千位上,由于百位没有向千位借位(或借位后已还原),所以$1 - □ = 1$,这里的$□$应为$0$。但同样,我们更关心如何通过结果来确定减数的千位。由于这是一个三位数减三位数的竖式,且结果仍为三位数(或可看作省略了万位$0$的三位数),所以减数的千位不能使结果变为两位数。因此,减数的千位应小于或等于被减数的千位(这里被减数千位是$1$,但由于是最高位且不可能为$0$,所以实际分析时考虑的是它作为有效数字的位置)。由于结果千位为$1$,且没有向万位借位,所以减数的千位只能是$0$(使得$1 - 0 = 1$)。但这里我们实际上是通过结果和竖式的结构来反推,更直接的方法是看除式的商。
由于$360 ÷ □□ = 15$,可以通过试除或分解质因数来找到除数。但这里我们直接给出答案:除数是$24$(因为$360 ÷ 15 = 24$)。
所以,第二个竖式填完后(只关注减法部分,除式用于验证)为:
$\begin{array}{r r r r}&1&5 \\ \hline &3&6&0 \\ -&2&□&0 \\ \hline &1&□&0 \end{array}$
进一步补全得(注意这里我们实际上是通过除式的结果来补全减法的减数):
$\begin{array}{r r r r}&1&5 \\ \hline &3&6&0 \\ -&2&4&0 \\ \hline &1&2&0 \end{array}$
(减数为$240$,与除式$360 ÷ 15 = 24$中的除数$24$(看作$240$除以$10$的简化形式)相对应)
答案:
第一个竖式:
$\begin{array}{r r r r r}&2&3 \\ \hline &2&3&5&0&6 \\ -&2&2&4&0 \\ \hline &&&4&6 \\ -&4&6\\ \hline &&&0\end{array}$
第二个竖式(答案不唯一,因为十位和百位的$□$可以相同且为$0-9$内的任何数字,但这里给出的是通过除式反推得出的答案):
$\begin{array}{r r r r}&1&5 \\ \hline &3&6&0 \\ -&2&4&0 \\ \hline &1&2&0 \end{array}$
第一个竖式:
从个位开始分析,$6 - 0 = 6$,所以下方的减数个位是$0$(已给出)。
十位上,$□ - 4 = 6$,显然这里的$□$应该是$0$(向百位借$1$后变为$10 - 4 = 6$),同时百位的$5$被借走$1$变为$4$。
百位上,$4 - □ = 4$,所以减数的百位$□$应该是$0$(但考虑到十位借位的情况,实际应为$4 - 0(借位后仍为原数)- 4 = 0$,即不借位时直接相等),但这里我们主要关注十位的借位情况,百位直接相减得出$0$。
由于十位需要借位,千位的$2$减去减数千位的数字后必须仍能保持为$2$(或经过借位后变为$2$),显然减数千位应为$0$(不借位)或小于$2$的数(借位后),但考虑到最高位不能是$0$,且需要借位使得十位能够进行$10 - 4$的运算,所以这里的借位应来自百位向千位的借位(即把$2$看成$1$后借$1$给百位,自己变为$1$,但由于减数千位是$0$,所以$1 - 0 = 1$,再向万位借$1$后变为$2$),但直接分析可知减数千位填$0$,万位$2$落下即可(因为不涉及万位的运算)。但简化分析,我们直接看千位结果,$2 - 0(考虑借位后的实际影响)= 2$(或理解为$2$减去任何小于它的正整数后,通过借位都能保持为$2$或更大的数,但这里只关心结果为$2$,所以填$0$),所以千位$□$填$3$(这是通过$46 ÷ 23 = 2$反推得出的除数)。
所以,第一个竖式填完后为:
$\begin{array}{r r r r}&2&3 \\ \hline &2&□&5&0&6 \\ -&-&-&4&0 \\ \hline &-&-&4&6 \end{array}$
(其中下方的减数按借位分析后应为$040$,但最高位$0$不写,且由于我们是从结果反推,所以直接写$40$表示十位和百位的减数,千位已知为$0$,万位$2$落下即可)
进一步补全得:
$\begin{array}{r r r r}&2&3 \\ \hline &2&3&5&0&6 \\ -&2&2&4&0 \\ \hline &&&4&6 \\ -&4&6\\ \hline &&&0\end{array}$
(注意这里的$2240$是通过分析得出的实际减数,与最初的$□4□0$对应)
第二个竖式:
同样从个位开始,$0 - 0 = 0$,所以减数的个位是$0$(已给出,此步实际不产生新信息)。
十位上,由于结果为$0$,且没有向百位借位(因为百位结果也是确定的数字,且没有进一步的借位标记),所以$□ - □ = 0$,即两个$□$内的数字相同。但由于我们是从结果反推,且知道这是一个减法竖式,所以更关心的是如何通过结果来确定这些$□$。
百位上,$□ - 2 = 1$(考虑十位可能借位,但此处分析可暂不考虑借位,因为结果已给出),所以被减数的百位$□$应为$3$($3 - 2 = 1$)。
千位上,由于百位没有向千位借位(或借位后已还原),所以$1 - □ = 1$,这里的$□$应为$0$。但同样,我们更关心如何通过结果来确定减数的千位。由于这是一个三位数减三位数的竖式,且结果仍为三位数(或可看作省略了万位$0$的三位数),所以减数的千位不能使结果变为两位数。因此,减数的千位应小于或等于被减数的千位(这里被减数千位是$1$,但由于是最高位且不可能为$0$,所以实际分析时考虑的是它作为有效数字的位置)。由于结果千位为$1$,且没有向万位借位,所以减数的千位只能是$0$(使得$1 - 0 = 1$)。但这里我们实际上是通过结果和竖式的结构来反推,更直接的方法是看除式的商。
由于$360 ÷ □□ = 15$,可以通过试除或分解质因数来找到除数。但这里我们直接给出答案:除数是$24$(因为$360 ÷ 15 = 24$)。
所以,第二个竖式填完后(只关注减法部分,除式用于验证)为:
$\begin{array}{r r r r}&1&5 \\ \hline &3&6&0 \\ -&2&□&0 \\ \hline &1&□&0 \end{array}$
进一步补全得(注意这里我们实际上是通过除式的结果来补全减法的减数):
$\begin{array}{r r r r}&1&5 \\ \hline &3&6&0 \\ -&2&4&0 \\ \hline &1&2&0 \end{array}$
(减数为$240$,与除式$360 ÷ 15 = 24$中的除数$24$(看作$240$除以$10$的简化形式)相对应)
答案:
第一个竖式:
$\begin{array}{r r r r r}&2&3 \\ \hline &2&3&5&0&6 \\ -&2&2&4&0 \\ \hline &&&4&6 \\ -&4&6\\ \hline &&&0\end{array}$
第二个竖式(答案不唯一,因为十位和百位的$□$可以相同且为$0-9$内的任何数字,但这里给出的是通过除式反推得出的答案):
$\begin{array}{r r r r}&1&5 \\ \hline &3&6&0 \\ -&2&4&0 \\ \hline &1&2&0 \end{array}$
+跟踪练习3在□里填合适的数字。


答案:




例1 用简便方法计算下面各题。
$400 ÷ 25$ $270 ÷ 54$
$400 ÷ 25$ $270 ÷ 54$
答案:解析:
第一个算式 $400 ÷ 25$ 可以通过商不变的规律,把被除数和除数都乘4,使除数变成100,从而简化计算。
第二个算式 $270 ÷ 54$ 可以先把被除数和除数都除以9,将较大的数转化成较小的数,再计算比较简便。
答案:
$400 ÷ 25$
$= (400 × 4) ÷ (25 × 4)$
$= 1600 ÷ 100$
$= 16$
$270 ÷ 54$
$= (270 ÷ 9) ÷ (54 ÷ 9)$
$= 30 ÷ 6$
$= 5$
第一个算式 $400 ÷ 25$ 可以通过商不变的规律,把被除数和除数都乘4,使除数变成100,从而简化计算。
第二个算式 $270 ÷ 54$ 可以先把被除数和除数都除以9,将较大的数转化成较小的数,再计算比较简便。
答案:
$400 ÷ 25$
$= (400 × 4) ÷ (25 × 4)$
$= 1600 ÷ 100$
$= 16$
$270 ÷ 54$
$= (270 ÷ 9) ÷ (54 ÷ 9)$
$= 30 ÷ 6$
$= 5$