6. (生活体验)购物。
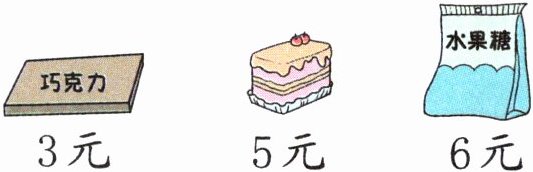
(1)小冬带的钱正好可以买4块蛋糕,小冬带了多少元？
(2)亮亮买了同一种食品,正好用了18元,他买的可能是什么？
(3)天天有15元,买了一块巧克力后,还剩多少元？剩下的钱还能买几袋水果糖？
(4)你还能提出其他用除法计算的问题并解答吗？
(1)小冬带的钱正好可以买4块蛋糕,小冬带了多少元？
(2)亮亮买了同一种食品,正好用了18元,他买的可能是什么？
(3)天天有15元,买了一块巧克力后,还剩多少元？剩下的钱还能买几袋水果糖？
(4)你还能提出其他用除法计算的问题并解答吗？
答案：（1）$5×4=20$（元）
（2）$18÷3=6$（块） $18÷6=3$（袋）
他买的可能是 6 块巧克力或 3 袋水果糖
（3）$15-3=12$（元） $12÷6=2$（袋）
（4）答案不唯一，如买一袋水果糖的钱能买几块巧克力？ $6÷3=2$（块）
（2）$18÷3=6$（块） $18÷6=3$（袋）
他买的可能是 6 块巧克力或 3 袋水果糖
（3）$15-3=12$（元） $12÷6=2$（袋）
（4）答案不唯一，如买一袋水果糖的钱能买几块巧克力？ $6÷3=2$（块）
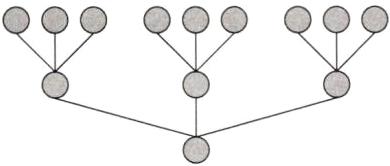
7. (思维过程)商店为了促销,规定3个空瓶可以换1瓶饮料。丁叔叔买了9瓶饮料,他实际可以喝多少瓶？
思路提示：用1个“$◯$”表示1瓶饮料,按3个空瓶换1瓶饮料逐次换下去。
思路提示：用1个“$◯$”表示1瓶饮料,按3个空瓶换1瓶饮料逐次换下去。
答案：
$9÷3=3$（瓶） $3÷3=1$（瓶）
$9+3+1=13$（瓶）
解析：如图，用 1 个
表示 1 瓶饮料，3 个空瓶换 1 瓶饮料，9 瓶里面有 3 个 3 瓶，则 9 瓶喝完能换 3 瓶饮料，3 瓶喝完又能换 1 瓶饮料，所以实际可以喝 $9+3+1=13$（瓶）饮料。
$9÷3=3$（瓶） $3÷3=1$（瓶）
$9+3+1=13$（瓶）
解析：如图，用 1 个
表示 1 瓶饮料，3 个空瓶换 1 瓶饮料，9 瓶里面有 3 个 3 瓶，则 9 瓶喝完能换 3 瓶饮料，3 瓶喝完又能换 1 瓶饮料，所以实际可以喝 $9+3+1=13$（瓶）饮料。8. (推理意识)
思路提示：可以把第一道算式看成一个整体代入第二道算式中。
思路提示：可以把第一道算式看成一个整体代入第二道算式中。
答案：
6 3 解析：对比第一、二道算式，可以发现第二道算式中多了 2 个
，即多了 6，因此
=$6÷2=3$，再将
$=3$ 代入第一道算式中，可得
+
+$3+3+3=21$，即
$×2=12$，所以
=$12÷2=6$。
6 3 解析：对比第一、二道算式，可以发现第二道算式中多了 2 个
，即多了 6，因此=$6÷2=3$，再将 $=3$ 代入第一道算式中，可得++$3+3+3=21$，即 $×2=12$，所以=$12÷2=6$。9. $◯ + ◯ + ◯ + ◯ + ◯ + \lozenge + \lozenge = 22$
$◯ + \lozenge = 5$
$◯ = (\quad)$ $\lozenge = (\quad)$
思路提示：可以把第二道算式看成一个整体,分两次代入第一道算式中。
$◯ + \lozenge = 5$
$◯ = (\quad)$ $\lozenge = (\quad)$
思路提示：可以把第二道算式看成一个整体,分两次代入第一道算式中。
答案：
4 1 解析：把第二道算式看成一个整体，第一道算式中的
+
+
+
可以看成两组
+
，即 $5×2=10$，从第一道算式中去掉
+
+
+
，即 $22-10=12$，所以
+
+
$=12$，即
$×3=12$，则
=$12÷3=4$，再根据
+
$=5$，可得
=$5-4=1$。
整体代入法是一种在数学解题中常用的方法，本题将一道算式看成一个整体代入到另一道算式中，从而简化问题，使求解过程更加直观和简便。
4 1 解析：把第二道算式看成一个整体，第一道算式中的
+++ 可以看成两组+，即 $5×2=10$，从第一道算式中去掉+++，即 $22-10=12$，所以++ $=12$，即 $×3=12$，则=$12÷3=4$，再根据+ $=5$，可得=$5-4=1$。整体代入法是一种在数学解题中常用的方法，本题将一道算式看成一个整体代入到另一道算式中，从而简化问题，使求解过程更加直观和简便。