9.如图,是圆柱的有
③④
,是棱柱的有②⑤⑥
.(填序号)答案:③④ ②⑤⑥
10.用棱长相同的小正方体摆成如图所示的几何体,第1层有1个正方体,第2层有3个正方体,第3层有6个正方体,按图中摆放的方法类推,第10层有
55
个正方体.答案:55
解析:
第1层:1个
第2层:1+2=3个
第3层:1+2+3=6个
...
第10层:1+2+3+...+10=$\frac{10×(10+1)}{2}=55$个
55
第2层:1+2=3个
第3层:1+2+3=6个
...
第10层:1+2+3+...+10=$\frac{10×(10+1)}{2}=55$个
55
11.8个立体图形如图所示.
(1)找出与图形①具有相同特征的图形,并指出相同的特征是什么;
(2)找出其他具有相同特征的图形,并指出相同的特征是什么.
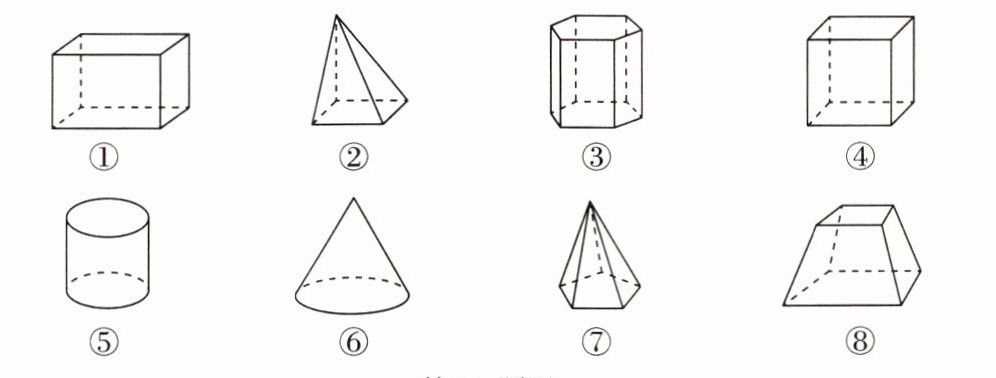
(1)找出与图形①具有相同特征的图形,并指出相同的特征是什么;
(2)找出其他具有相同特征的图形,并指出相同的特征是什么.

答案:解:(1)与图形①具有相同特征的图形有③④⑤,相同的特征是它们都是柱体.(2)图形②⑥⑦是具有相同特征的图形,相同的特征是它们都是锥体.
12.如图是一个“粮仓”的示意图.请根据图中数据求出“粮仓”的容积.($V_{圆柱}= πr^{2}h,V_{圆锥}= \frac {1}{3}πr^{2}h$)


答案:解:根据圆柱和圆锥的体积公式,得V粮仓=V圆柱+V圆锥=π×$(\frac{6}{2})^{2}$×4+$\frac{1}{3}$π×$(\frac{6}{2})^{2}$×(7-4)=36π+9π=45π.答:"粮仓"的容积为45π.
解析:
解:$V_{粮仓}=V_{圆柱}+V_{圆锥}$
$=\pi×(\frac{6}{2})^{2}×4+\frac{1}{3}\pi×(\frac{6}{2})^{2}×(7 - 4)$
$=\pi×3^{2}×4+\frac{1}{3}\pi×3^{2}×3$
$=36\pi + 9\pi$
$=45\pi$
答:“粮仓”的容积为$45\pi$。
$=\pi×(\frac{6}{2})^{2}×4+\frac{1}{3}\pi×(\frac{6}{2})^{2}×(7 - 4)$
$=\pi×3^{2}×4+\frac{1}{3}\pi×3^{2}×3$
$=36\pi + 9\pi$
$=45\pi$
答:“粮仓”的容积为$45\pi$。
13.如图,四个几何体分别是三棱柱、四棱柱、五棱柱和六棱柱,三棱柱有5个面,9条棱,6个顶点.观察图形,填空.
(1)四棱柱有
(2)六棱柱有
(3)由此猜想,n棱柱有


(1)四棱柱有
6
个面,12
条棱,8
个顶点;(2)六棱柱有
8
个面,18
条棱,12
个顶点;(3)由此猜想,n棱柱有
n+2
个面,3n
条棱,2n
个顶点.

答案:(1)6 12 8 (2)8 18 12 (3)n+2 3n 2n