6. 将如图所示的长方形绕它的对角线所在直线旋转一周,形成的几何体是(
B
)答案:B
7. 国扇文化有着深厚的文化底蕴,历来中国有“制扇王国”之称. 打开折扇时,随着扇骨的移动形成了一个扇面,这种现象可以用数学原理解释为
线动成面
.答案:线动成面
8. (2024秋·罗湖区期中)已知一个直角三角形的两直角边长分别是3和4,将这个直角三角形绕它的直角边所在直线旋转一周,可以得到圆锥,则圆锥的体积是______.($V_{圆锥}= \frac{1}{3}\pi r^{2}h$,结果保留$\pi$)
12π或16π
答案:12π或16π
解析:
情况一:绕直角边为3所在直线旋转一周
此时圆锥底面半径$r = 4$,高$h = 3$
$V=\frac{1}{3}\pi r^{2}h=\frac{1}{3}\pi×4^{2}×3=\frac{1}{3}\pi×16×3 = 16\pi$
情况二:绕直角边为4所在直线旋转一周
此时圆锥底面半径$r = 3$,高$h = 4$
$V=\frac{1}{3}\pi r^{2}h=\frac{1}{3}\pi×3^{2}×4=\frac{1}{3}\pi×9×4 = 12\pi$
12π或16π
此时圆锥底面半径$r = 4$,高$h = 3$
$V=\frac{1}{3}\pi r^{2}h=\frac{1}{3}\pi×4^{2}×3=\frac{1}{3}\pi×16×3 = 16\pi$
情况二:绕直角边为4所在直线旋转一周
此时圆锥底面半径$r = 3$,高$h = 4$
$V=\frac{1}{3}\pi r^{2}h=\frac{1}{3}\pi×3^{2}×4=\frac{1}{3}\pi×9×4 = 12\pi$
12π或16π
9. 小明学习了“面动成体”之后,他用一个边长分别为$3cm$,$4cm和5cm$的直角三角形,绕其中一条边所在直线旋转一周,得到了一个几何体.
(1)请画出可能得到的几何体的简图;
(2)分别计算出这些几何体的体积.
(1)请画出可能得到的几何体的简图;
(2)分别计算出这些几何体的体积.
答案:
解:(1)几何体简图如答图所示(单位:cm).

(2)如答图①,以4cm长的边所在直线为轴,体积为
$\frac{1}{3}×π×3^{2}×4=12π(cm^{3})$;
如答图②,以3cm长的边所在直线为轴,体积为
$\frac{1}{3}×π×4^{2}×3=16π(cm^{3})$;
如答图③,以5cm长的边所在直线为轴,体积为
$\frac{1}{3}×π×(\frac{12}{5})^{2}×5=9.6π(cm^{3})$.
解:(1)几何体简图如答图所示(单位:cm).

(2)如答图①,以4cm长的边所在直线为轴,体积为
$\frac{1}{3}×π×3^{2}×4=12π(cm^{3})$;
如答图②,以3cm长的边所在直线为轴,体积为
$\frac{1}{3}×π×4^{2}×3=16π(cm^{3})$;
如答图③,以5cm长的边所在直线为轴,体积为
$\frac{1}{3}×π×(\frac{12}{5})^{2}×5=9.6π(cm^{3})$.
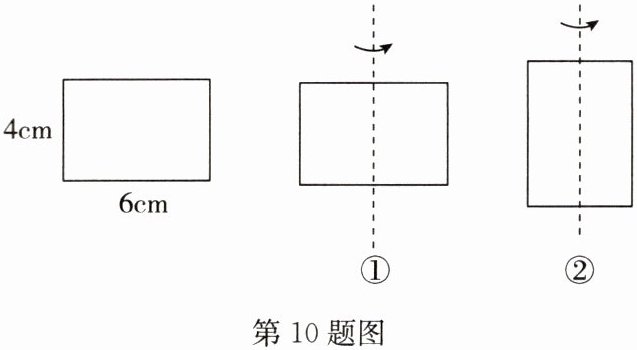
10. 如图,有一个长$6cm$、宽$4cm$的长方形纸板,现要求以其一组对边中点所在直线为轴旋转$180^{\circ}$,可按两种方案进行操作.
方案一:以较长的一组对边中点所在直线为轴旋转,如图①.
方案二:以较短的一组对边中点所在直线为轴旋转,如图②.
(1)上述操作形成的几何体是______
(2)请通过计算说明按哪种方案得到的几何体的体积较大.
方案一:以较长的一组对边中点所在直线为轴旋转,如图①.
方案二:以较短的一组对边中点所在直线为轴旋转,如图②.
(1)上述操作形成的几何体是______
圆柱
______,说明的事实是______面动成体
______;(2)请通过计算说明按哪种方案得到的几何体的体积较大.

(2)解:方案一:$π×3^{2}×4=36π(cm^{3})$,
方案二:$π×2^{2}×6=24π(cm^{3})$,
因为$36π>24π$,
所以按方案一得到的几何体的体积较大.
方案二:$π×2^{2}×6=24π(cm^{3})$,
因为$36π>24π$,
所以按方案一得到的几何体的体积较大.
答案:(1)圆柱 面动成体
(2)解:方案一:$π×3^{2}×4=36π(cm^{3})$,
方案二:$π×2^{2}×6=24π(cm^{3})$,
因为$36π>24π$,
所以按方案一得到的几何体的体积较大.
(2)解:方案一:$π×3^{2}×4=36π(cm^{3})$,
方案二:$π×2^{2}×6=24π(cm^{3})$,
因为$36π>24π$,
所以按方案一得到的几何体的体积较大.