10. 把下列各式因式分解:
(1) $8a^{4}-2a^{2}b^{2}$;
(2) $4x^{3}y - 4x^{2}y^{2}+xy^{3}$;
(3) $m^{2}(n - 2)+25(2 - n)$;
(4) $(a^{2}+b^{2}-c^{2})^{2}-4a^{2}b^{2}$;
(5) $45am^{2}-20ax^{2}+20axy - 5ay^{2}$;
(6) $4a^{2}+4a - 4a^{2}b - b - 4ab + 1$。
(1) $8a^{4}-2a^{2}b^{2}$;
(2) $4x^{3}y - 4x^{2}y^{2}+xy^{3}$;
(3) $m^{2}(n - 2)+25(2 - n)$;
(4) $(a^{2}+b^{2}-c^{2})^{2}-4a^{2}b^{2}$;
(5) $45am^{2}-20ax^{2}+20axy - 5ay^{2}$;
(6) $4a^{2}+4a - 4a^{2}b - b - 4ab + 1$。
答案:
(1)原式=2a²(4a²-b²)=2a²(2a-b)(2a+b).
(2)原式=xy(4x²-4xy+y²)=xy(2x-y)².
(3)原式=m²(n-2)-25(n-2)=(n-2)(m²-25)=(n-2)(m+5)(m-5).
(4)原式=(a²+b²-c²+2ab)(a²+b²-c²-2ab)=[(a+b)²-c²][(a-b)²-c²]=(a+b+c)(a+b-c)(a-b+c)(a-b-c).
(5)原式=45am²-5a(4x²-4xy+y²)=5a[9m²-(2x-y)²]=5a(3m-2x+y)(3m+2x-y).
(6)原式=(4a²+4a+1)-b(4a²+4a+1)=(2a+1)²(1-b).
(1)原式=2a²(4a²-b²)=2a²(2a-b)(2a+b).
(2)原式=xy(4x²-4xy+y²)=xy(2x-y)².
(3)原式=m²(n-2)-25(n-2)=(n-2)(m²-25)=(n-2)(m+5)(m-5).
(4)原式=(a²+b²-c²+2ab)(a²+b²-c²-2ab)=[(a+b)²-c²][(a-b)²-c²]=(a+b+c)(a+b-c)(a-b+c)(a-b-c).
(5)原式=45am²-5a(4x²-4xy+y²)=5a[9m²-(2x-y)²]=5a(3m-2x+y)(3m+2x-y).
(6)原式=(4a²+4a+1)-b(4a²+4a+1)=(2a+1)²(1-b).
11. 操作与思考:一张边长为 $a$ 的正方形桌面,因为实际需要,要将正方形边长增加 $b$,从而得到一个更大的正方形,木工师傅设计了如图所示的方案。
(1)请用数学式子表示图中的等量关系:
(2)请你利用(2)中的结论计算 $2×20.18^{2}+80.72×19.82+2×19.82^{2}$。
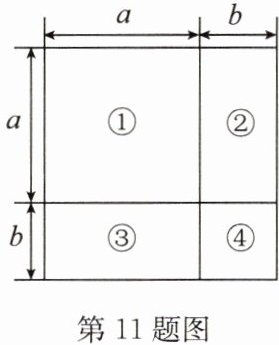
(1)请用数学式子表示图中的等量关系:
$(a+b)^2=a^2+2ab+b^2$
。(2)请你利用(2)中的结论计算 $2×20.18^{2}+80.72×19.82+2×19.82^{2}$。

解:原式=2×20.18²+2×2×20.18×19.82+2×19.82²=2×(20.18+19.82)²=2×40²=3200.
答案:
(1)(a+b)²=a²+2ab+b²
(2)解:原式=2×20.18²+2×2×20.18×19.82+2×19.82²=2×(20.18+19.82)²=2×40²=3200.
(1)(a+b)²=a²+2ab+b²
(2)解:原式=2×20.18²+2×2×20.18×19.82+2×19.82²=2×(20.18+19.82)²=2×40²=3200.
12. 八年级课外兴趣小组活动时,老师提出了如下问题:将 $2a - 3ab - 4 + 6b$ 因式分解。
【观察】经过小组合作交流,小明得到了如下的解决方法:
解法一:原式 $=(2a - 3ab)-(4 - 6b)= a(2 - 3b)-2(2 - 3b)= (2 - 3b)(a - 2)$。
解法二:原式 $=(2a - 4)-(3ab - 6b)= 2(a - 2)-3b(a - 2)= (a - 2)(2 - 3b)$。
【类比】(1)请用分组分解法将 $x^{2}-a^{2}+x + a$ 因式分解;
【挑战】(2)请用分组分解法将 $ax + a^{2}-2ab - bx + b^{2}$ 因式分解;
(3)若 $a^{2}+b^{2}= 9,a - b = 2$,请用分组分解法先将 $a^{4}-2a^{3}b + 2a^{2}b^{2}-2ab^{3}+b^{4}$ 因式分解,再求值。
【观察】经过小组合作交流,小明得到了如下的解决方法:
解法一:原式 $=(2a - 3ab)-(4 - 6b)= a(2 - 3b)-2(2 - 3b)= (2 - 3b)(a - 2)$。
解法二:原式 $=(2a - 4)-(3ab - 6b)= 2(a - 2)-3b(a - 2)= (a - 2)(2 - 3b)$。
【类比】(1)请用分组分解法将 $x^{2}-a^{2}+x + a$ 因式分解;
【挑战】(2)请用分组分解法将 $ax + a^{2}-2ab - bx + b^{2}$ 因式分解;
(3)若 $a^{2}+b^{2}= 9,a - b = 2$,请用分组分解法先将 $a^{4}-2a^{3}b + 2a^{2}b^{2}-2ab^{3}+b^{4}$ 因式分解,再求值。
答案:
(1)x²-a²+x+a=(x²-a²)+(x+a)=(x+a)(x-a)+(x+a)=(x+a)(x-a+1).
(2)ax+a²-2ab-bx+b²=(a²-2ab+b²)+(ax-bx)=(a-b)²+(a-b)x=(a-b)(a-b+x).
(3)a⁴-2a³b+2a²b²-2ab³+b⁴=(a⁴+2a²b²+b⁴)-(2a³b+2ab³)=(a²+b²)²-2ab(a²+b²)=(a²+b²)(a²-2ab+b²)=(a²+b²)(a-b)².当a²+b²=9,a-b=2时,原式=9×4=36.
(1)x²-a²+x+a=(x²-a²)+(x+a)=(x+a)(x-a)+(x+a)=(x+a)(x-a+1).
(2)ax+a²-2ab-bx+b²=(a²-2ab+b²)+(ax-bx)=(a-b)²+(a-b)x=(a-b)(a-b+x).
(3)a⁴-2a³b+2a²b²-2ab³+b⁴=(a⁴+2a²b²+b⁴)-(2a³b+2ab³)=(a²+b²)²-2ab(a²+b²)=(a²+b²)(a²-2ab+b²)=(a²+b²)(a-b)².当a²+b²=9,a-b=2时,原式=9×4=36.