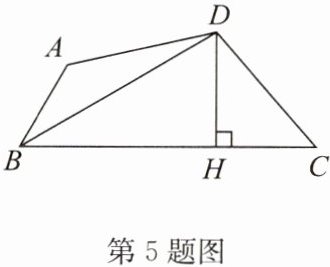
5. 如图,在四边形$ABCD$中,$BC > DA$,$AD = DC$,$BD平分\angle ABC$,$DH \perp BC于点H$.
求证:(1)$\angle DAB + \angle C = 180^{\circ}$;
(2)$BH = \frac{1}{2}(AB + BC)$.
求证:(1)$\angle DAB + \angle C = 180^{\circ}$;
(2)$BH = \frac{1}{2}(AB + BC)$.

答案:
(1)证明:如答图,过点D作DE⊥AB,交BA的延长线于点E.
∵BD平分∠ABC,DH⊥BC,
∴DH=DE.
在Rt△ADE和Rt△CDH中,{DA=DC,DE=DH,
∴Rt△ADE≌Rt△CDH(HL),
∴∠C=∠DAE.
∵∠DAB+∠DAE=180°,
∴∠DAB+∠C=180°.
(2)在Rt△BDE和Rt△BDH中,{BD=BD,DE=DH,
∴Rt△BDE≌Rt△BDH(HL),
∴BE=BH.
∵Rt△ADE≌Rt△CDH,
∴AE=CH,
∴AB+BC=AB+BH+CH=BE+BH=2BH,
∴BH=$\frac{1}{2}$(AB+BC).
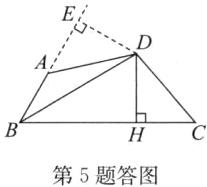
(1)证明:如答图,过点D作DE⊥AB,交BA的延长线于点E.
∵BD平分∠ABC,DH⊥BC,
∴DH=DE.
在Rt△ADE和Rt△CDH中,{DA=DC,DE=DH,
∴Rt△ADE≌Rt△CDH(HL),
∴∠C=∠DAE.
∵∠DAB+∠DAE=180°,
∴∠DAB+∠C=180°.
(2)在Rt△BDE和Rt△BDH中,{BD=BD,DE=DH,
∴Rt△BDE≌Rt△BDH(HL),
∴BE=BH.
∵Rt△ADE≌Rt△CDH,
∴AE=CH,
∴AB+BC=AB+BH+CH=BE+BH=2BH,
∴BH=$\frac{1}{2}$(AB+BC).

6. 如图,$CA = CB$,$CD = CE$,$\angle ACB = \angle DCE$,$AD$,$BE交于点H$,连接$CH$.
求证:(1)$\triangle ACD \cong \triangle BCE$;
(2)$HC平分\angle AHE$.

求证:(1)$\triangle ACD \cong \triangle BCE$;
(2)$HC平分\angle AHE$.

答案:
(1)证明:
∵∠ACB=∠DCE,
∴∠ACD=∠BCE.
在△ACD和△BCE中,{CA=CB,∠ACD=∠BCE,CD=CE,
∴△ACD≌△BCE(SAS).
(2)如答图,过点C作CM⊥AD于点M,CN⊥BE于点N.

∵△ACD≌△BCE,
∴∠CAM=∠CBN,
在△ACM和△BCN中,{∠CAM=∠CBN,∠AMC=∠BNC=90°,AC=BC,
∴△ACM≌△BCN,
∴CM=CN.
又CM⊥AH,CN⊥HE,
∴HC平分∠AHE;
(1)证明:
∵∠ACB=∠DCE,
∴∠ACD=∠BCE.
在△ACD和△BCE中,{CA=CB,∠ACD=∠BCE,CD=CE,
∴△ACD≌△BCE(SAS).
(2)如答图,过点C作CM⊥AD于点M,CN⊥BE于点N.

∵△ACD≌△BCE,
∴∠CAM=∠CBN,
在△ACM和△BCN中,{∠CAM=∠CBN,∠AMC=∠BNC=90°,AC=BC,
∴△ACM≌△BCN,
∴CM=CN.
又CM⊥AH,CN⊥HE,
∴HC平分∠AHE;