22. (6分)如图,锐角$\triangle ABC的两条高BD$,$CE相交于点O$,且$OB = OC$。
(1)求证:$\triangle ABC$是等腰三角形;
(2)判断点$O是否在\angle BAC$的平分线上,并说明理由。

(1)求证:$\triangle ABC$是等腰三角形;
(2)判断点$O是否在\angle BAC$的平分线上,并说明理由。

答案:
(1)证明:∵OB=OC,∴∠OBC=∠OCB.
∵锐角△ABC的两条高BD,CE相交于点O,
∴∠BEC=∠CDB=90°.
∵∠BEC+∠BCE+∠ABC=∠CDB+∠DBC+∠ACB=180°,
∴180°−∠BEC−∠BCE=180°−∠CDB−∠DBC,
∴∠ABC=∠ACB,∴AB=AC,∴△ABC是等腰三角形
(2)解:点O在∠BAC的平分线上.
理由:连接AO,如答图.

在△AOB和△AOC中,$\begin{cases}AB = AC\\OB = OC\\OA = OA\end{cases}$
∴△AOB≌△AOC(SSS),∴∠BAO=∠CAO,
∴点O在∠BAC的平分线上.
(1)证明:∵OB=OC,∴∠OBC=∠OCB.
∵锐角△ABC的两条高BD,CE相交于点O,
∴∠BEC=∠CDB=90°.
∵∠BEC+∠BCE+∠ABC=∠CDB+∠DBC+∠ACB=180°,
∴180°−∠BEC−∠BCE=180°−∠CDB−∠DBC,
∴∠ABC=∠ACB,∴AB=AC,∴△ABC是等腰三角形
(2)解:点O在∠BAC的平分线上.
理由:连接AO,如答图.

在△AOB和△AOC中,$\begin{cases}AB = AC\\OB = OC\\OA = OA\end{cases}$
∴△AOB≌△AOC(SSS),∴∠BAO=∠CAO,
∴点O在∠BAC的平分线上.
23. (9分)如图,在$\triangle OBC$中,边$BC的垂直平分线交\angle BOC的平分线于点D$,连接$DB$,$DC$,过点$D作DF\perp OC于点F$。
(1)若$\angle BOC = 60^{\circ}$,求$\angle BDC$的度数;
(2)若$\angle BOC= \alpha$,则$\angle BDC= $______;(直接写出结果)
(3)求$OB$,$OC$,$OF$之间的数量关系。

(1)若$\angle BOC = 60^{\circ}$,求$\angle BDC$的度数;
(2)若$\angle BOC= \alpha$,则$\angle BDC= $______;(直接写出结果)
(3)求$OB$,$OC$,$OF$之间的数量关系。

答案:
(1)解:作DE⊥OB,交OB的延长线于点E,如答图.
∵OD平分∠BOC,DF⊥OC,点D在BC的垂直平分线上,∴DE=DF,∠DEB=∠DFC=90°,DB=DC.
在Rt△DEB和Rt△DFC中,$\begin{cases}DB = DC\\DE = DF\end{cases}$
∴Rt△DEB≌Rt△DFC(HL),
∴∠BDE=∠CDF,∴∠BDE+∠BDF=∠CDF+∠BDF,即∠EDF=∠BDC.
∵∠OED=∠OFD=90°,∠BOC=60°,∴∠EDF=120°,∴∠BDC=120°.

(2)180°−α
(3)解:由(1)可知,△DEB≌△DFC,则BE=CF.
∵OB+OC=OB+OF+FC,
∴OB+OC=OB+OF+EB=(OB+EB)+OF=OE+OF.
在Rt△DEO和Rt△DFO中,$\begin{cases}OD = OD\\DE = DF\end{cases}$
∴Rt△DEO≌Rt△DFO(HL),
∴OE=OF,∴OB+OC=2OF.
(1)解:作DE⊥OB,交OB的延长线于点E,如答图.
∵OD平分∠BOC,DF⊥OC,点D在BC的垂直平分线上,∴DE=DF,∠DEB=∠DFC=90°,DB=DC.
在Rt△DEB和Rt△DFC中,$\begin{cases}DB = DC\\DE = DF\end{cases}$
∴Rt△DEB≌Rt△DFC(HL),
∴∠BDE=∠CDF,∴∠BDE+∠BDF=∠CDF+∠BDF,即∠EDF=∠BDC.
∵∠OED=∠OFD=90°,∠BOC=60°,∴∠EDF=120°,∴∠BDC=120°.

(2)180°−α
(3)解:由(1)可知,△DEB≌△DFC,则BE=CF.
∵OB+OC=OB+OF+FC,
∴OB+OC=OB+OF+EB=(OB+EB)+OF=OE+OF.
在Rt△DEO和Rt△DFO中,$\begin{cases}OD = OD\\DE = DF\end{cases}$
∴Rt△DEO≌Rt△DFO(HL),
∴OE=OF,∴OB+OC=2OF.
24. (12分)【了解概念】
定义:如果一个三角形一边上的中线等于这条边的一半,那么称这个三角形为“唯美三角形”,这条中线叫这条边的“唯美线”。
【理解运用】
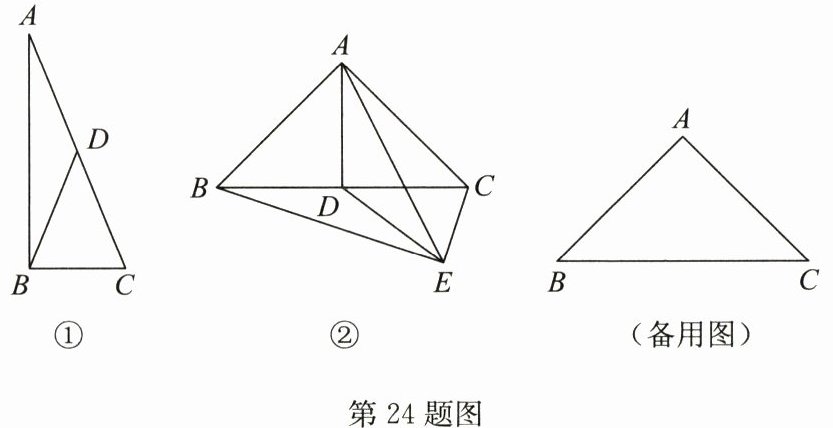
(1)如图①,$\triangle ABC$为“唯美三角形”,$BD为AC$边的“唯美线”,试判断$\triangle ABC$的形状,并说明理由。
【拓展提升】
(2)在$\triangle ABC$中,$AB = AC$,$E为\triangle ABC$外一点,连接$EB$,$EC$,若$\triangle ABC和\triangle EBC$均为“唯美三角形”,且$AD和ED分别为这两个三角形BC$边的“唯美线”。
①如图②,若点$E$,$A在直线BC$的异侧,连接$AE$,求$\angle AEB$的度数;
②若$E$为平面内一点,满足$EC = 3$,$EB = 9$,请求出点$A到BE$的距离。
定义:如果一个三角形一边上的中线等于这条边的一半,那么称这个三角形为“唯美三角形”,这条中线叫这条边的“唯美线”。
【理解运用】
(1)如图①,$\triangle ABC$为“唯美三角形”,$BD为AC$边的“唯美线”,试判断$\triangle ABC$的形状,并说明理由。
【拓展提升】
(2)在$\triangle ABC$中,$AB = AC$,$E为\triangle ABC$外一点,连接$EB$,$EC$,若$\triangle ABC和\triangle EBC$均为“唯美三角形”,且$AD和ED分别为这两个三角形BC$边的“唯美线”。
①如图②,若点$E$,$A在直线BC$的异侧,连接$AE$,求$\angle AEB$的度数;
②若$E$为平面内一点,满足$EC = 3$,$EB = 9$,请求出点$A到BE$的距离。

答案:
解:(1)结论:△ABC是直角三角形.
理由:∵△ABC为“唯美三角形”,BD为AC边的“唯美线”,∴DB=DC=DA,
∴∠DBC=∠C,∠DBA=∠A.
∵∠A+∠ABC+∠C=180°,
∴2∠ABD+2∠DBC=180°,
∴∠ABD+∠DBC=90°,
∴∠ABC=90°,∴△ABC是直角三角形.
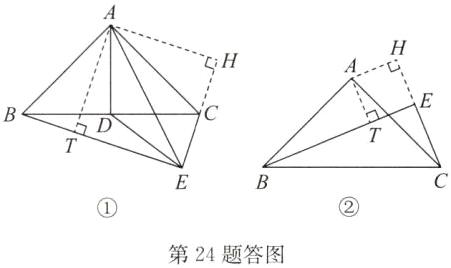
(2)①过点A作AH⊥EC交EC的延长线于点H,AT⊥BE于点T,如答图①.
∵△ABC和△EBC均为“唯美三角形”,且AD和ED 分别为这两个三角形BC边的“唯美线”,
∴DA=DB=DC=DE,△ABC,△BEC都是直角三角形,且∠BAC=∠BEC=90°.
∵AH⊥EH,AT⊥BE,∴∠ATE=∠H=∠TEH=90°,∴四边形ATEH是长方形,∴∠TAH=∠BAC=90°,∴∠BAT=∠CAH.
∵AB=AC,∠ATB=∠H=90°,
∴△ATB≌△AHC(AAS),∴AT=AH.
∵AH⊥EH,AT⊥BE,∴EA平分∠BEC,
∴∠AEB=$\frac{1}{2}$∠BEC=45°.
②当点E在BC的下方时,如答图①,
∵四边形ATEH是长方形,AT=AH,
∴四边形ATEH是正方形,∴ET=EH;
∵△ATB≌△AHC,∴BT=CH,
∴EB+EC=ET+BT+EH−CH=2ET=12,
∴ET=6,∴AT=6,即点A到BE的距离为6.
当点E在BC的上方时,如答图②,过点A作AH⊥EC 交EC的反向延长线于点H,AT⊥BE于点T.
同理可证△ABT≌△ACH,四边形ATEH是正方形,∴BT=CH,AT=ET=AH=EH,
∴BE−CE=BT+TE−(CH−EH)=2AT=9−3=6,∴AT=3,即点A到BE的距离为3.
综上所述,点A到BE的距离为6或3.
解:(1)结论:△ABC是直角三角形.
理由:∵△ABC为“唯美三角形”,BD为AC边的“唯美线”,∴DB=DC=DA,
∴∠DBC=∠C,∠DBA=∠A.
∵∠A+∠ABC+∠C=180°,
∴2∠ABD+2∠DBC=180°,
∴∠ABD+∠DBC=90°,
∴∠ABC=90°,∴△ABC是直角三角形.
(2)①过点A作AH⊥EC交EC的延长线于点H,AT⊥BE于点T,如答图①.
∵△ABC和△EBC均为“唯美三角形”,且AD和ED 分别为这两个三角形BC边的“唯美线”,
∴DA=DB=DC=DE,△ABC,△BEC都是直角三角形,且∠BAC=∠BEC=90°.
∵AH⊥EH,AT⊥BE,∴∠ATE=∠H=∠TEH=90°,∴四边形ATEH是长方形,∴∠TAH=∠BAC=90°,∴∠BAT=∠CAH.
∵AB=AC,∠ATB=∠H=90°,
∴△ATB≌△AHC(AAS),∴AT=AH.
∵AH⊥EH,AT⊥BE,∴EA平分∠BEC,
∴∠AEB=$\frac{1}{2}$∠BEC=45°.
②当点E在BC的下方时,如答图①,
∵四边形ATEH是长方形,AT=AH,
∴四边形ATEH是正方形,∴ET=EH;
∵△ATB≌△AHC,∴BT=CH,
∴EB+EC=ET+BT+EH−CH=2ET=12,
∴ET=6,∴AT=6,即点A到BE的距离为6.
当点E在BC的上方时,如答图②,过点A作AH⊥EC 交EC的反向延长线于点H,AT⊥BE于点T.
同理可证△ABT≌△ACH,四边形ATEH是正方形,∴BT=CH,AT=ET=AH=EH,
∴BE−CE=BT+TE−(CH−EH)=2AT=9−3=6,∴AT=3,即点A到BE的距离为3.
综上所述,点A到BE的距离为6或3.
