1. 角的平分线上的点到
角两边的距离
相等.答案：角两边的距离
2. 符号语言:
如图,∵∠AOC= ∠BOC,PD⊥OA,PE⊥OB,
∴
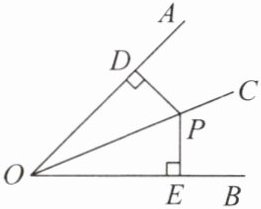
如图,∵∠AOC= ∠BOC,PD⊥OA,PE⊥OB,
∴
PD
=PE
.答案：PD PE
解析：
解：PD PE
1. 如图是利用尺规作∠AOB 的平分线 OC 的作法,在用尺规作角平分线时,用到的三角形全等的判定方法是 (
A.SSS
B.SAS
C.ASA
D.AAS
A
)A.SSS
B.SAS
C.ASA
D.AAS
答案：A
解析：
解：由尺规作图可知，OE=OD，EC=DC，OC=OC。在△OEC和△ODC中，OE=OD，EC=DC，OC=OC，根据SSS判定方法可得△OEC≌△ODC。
答案：A
答案：A
2. 如图,点 P 在∠AOB 的平分线上,点 P 到 OA 边的距离 PC= 10,Q 是 OB 边上的任意一点.下列选项正确的是 (
A.PQ＜10
B.PQ＞10
C.PQ≥10
D.PQ≤10
C
)A.PQ＜10
B.PQ＞10
C.PQ≥10
D.PQ≤10
答案：C
解析：
解：
∵点P在∠AOB的平分线上，PC⊥OA，PC=10，
∴点P到OB边的距离等于10（角平分线上的点到角两边距离相等）。
∵Q是OB边上任意一点，
∴PQ为点P到OB边上点Q的连线，其长度大于或等于点P到OB边的距离（垂线段最短）。
∴PQ≥10。
答案：C
∵点P在∠AOB的平分线上，PC⊥OA，PC=10，
∴点P到OB边的距离等于10（角平分线上的点到角两边距离相等）。
∵Q是OB边上任意一点，
∴PQ为点P到OB边上点Q的连线，其长度大于或等于点P到OB边的距离（垂线段最短）。
∴PQ≥10。
答案：C
3. 如图,在 Rt△ABC 中,∠C= 90°,以顶点 A 为圆心,以适当长为半径画弧,分别交 AC,AB 于点 M,N,再分别以点 M,N 为圆心,以大于$\frac{1}{2}MN $的长为半径画弧,两弧交于点 P,作射线 AP 交边 BC 于点 D.若 CD= 3,AB= 8,则△ABD 的面积是______
12
.答案：12
解析：
解：过点 D 作 DE⊥AB 于点 E。
由作图步骤可知，AP 是∠CAB 的平分线。
因为∠C=90°，DE⊥AB，
所以 DE=CD=3。
△ABD 的面积为：$\frac{1}{2}×AB×DE=\frac{1}{2}×8×3=12$。
12
由作图步骤可知，AP 是∠CAB 的平分线。
因为∠C=90°，DE⊥AB，
所以 DE=CD=3。
△ABD 的面积为：$\frac{1}{2}×AB×DE=\frac{1}{2}×8×3=12$。
12
4. 如图,BD 是△ABC 中∠ABC 的平分线,DE⊥AB 于点 E,DF⊥BC 于点 F.若 DE= 3,AB= 7,BC= 9,求△ABC 的面积.
答案：解:∵BD是∠ABC的平分线,DE⊥AB于点E,DF⊥BC于点F.∴DE=DF=3.∴S△ABC=S△ABD+S△BCD=$\frac{1}{2}$AB·DE+$\frac{1}{2}$BC·DF=$\frac{1}{2}$×7×3+$\frac{1}{2}$×9×3=24.
5. 如图,△ABC 的外角∠ACD 的平分线 CF 与∠ABC 的平分线 BG 相交于点 O.求证:点 O 到三边 AB,BC,AC 的距离相等.
答案：
证明:如答图,过点O作OM⊥BA交BA的延长线于点M,过点O作ON⊥BD于点N,过点O作OH⊥AC于点H.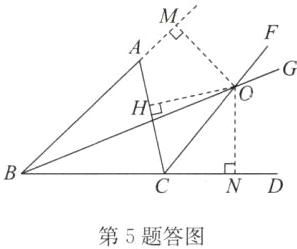
∵∠ACD的平分线CF与∠ABC的平分线BG交于点O,∴ON=OH,OM=ON,∴OM=ON=OH,即点O到三边AB，BC,AC的距离相等
证明:如答图,过点O作OM⊥BA交BA的延长线于点M,过点O作ON⊥BD于点N,过点O作OH⊥AC于点H.
∵∠ACD的平分线CF与∠ABC的平分线BG交于点O,∴ON=OH,OM=ON,∴OM=ON=OH,即点O到三边AB，BC,AC的距离相等