在解决最短路径问题时,我们通常利用
轴对称
、平移等变换把已知问题转化为容易解决的问题,从而作出最短路径的选择。答案:轴对称
1. 已知点A,点B都在直线l的上方,试用尺规作图在直线l上求作一点P,使得PA+PB的值最小,则下列作法中正确的是(
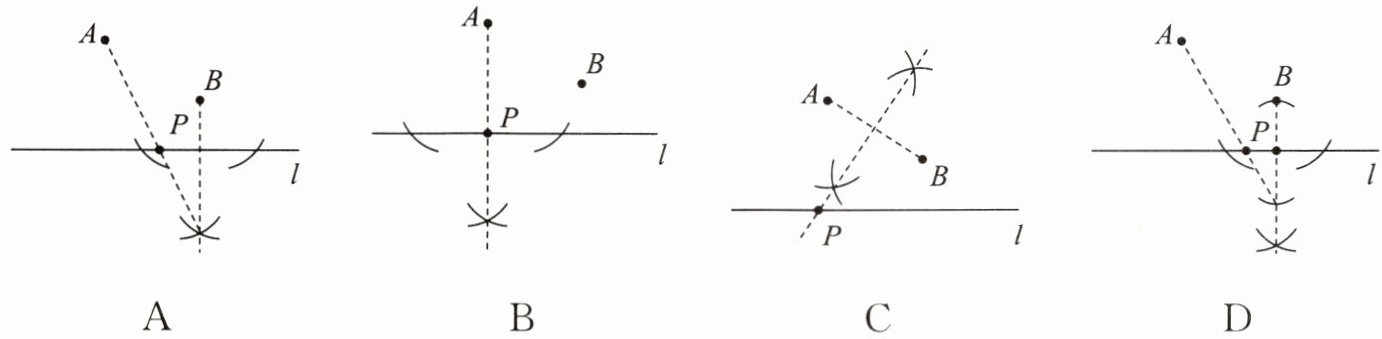
D
)
答案:D
2. 平行河岸两侧各有一城镇P,Q,根据发展规划,要修建一条公路连接P,Q两城镇.已知相同长度造桥总价远大于陆上公路造价,为了尽量减少总造价,应该选择方案(

C
)
答案:C
3. 如图,在△ABC中,AB= AC= 5,S_{△ABC}= 12,AD是△ABC的中线,F是AD上的动点,E是AC边上的动点,则CF+EF的最小值为(
A.3
B.$\frac{6}{5}$
C.$\frac{12}{5}$
D.$\frac{24}{5}$
D
)A.3
B.$\frac{6}{5}$
C.$\frac{12}{5}$
D.$\frac{24}{5}$
答案:D
解析:
解:
∵AB=AC=5,AD是△ABC的中线,
∴AD⊥BC,BD=DC。
设BC=2x,AD=h,由S△ABC=12得:
$\frac{1}{2} × 2x × h = 12 \Rightarrow xh=12$。
在Rt△ABD中,$x^2 + h^2 = 5^2 = 25$。
联立得$x^2 + (\frac{12}{x})^2 = 25$,解得$x=3$($x=4$舍),则BC=6,AD=4。
作点C关于AD的对称点B,连接BE交AD于F,则CF=BF,CF+EF=BF+EF=BE。
当BE⊥AC时,BE最小。
由S△ABC=$\frac{1}{2} × AC × BE=12$,得$\frac{1}{2} × 5 × BE=12 \Rightarrow BE=\frac{24}{5}$。
故CF+EF的最小值为$\frac{24}{5}$。
答案:D
∵AB=AC=5,AD是△ABC的中线,
∴AD⊥BC,BD=DC。
设BC=2x,AD=h,由S△ABC=12得:
$\frac{1}{2} × 2x × h = 12 \Rightarrow xh=12$。
在Rt△ABD中,$x^2 + h^2 = 5^2 = 25$。
联立得$x^2 + (\frac{12}{x})^2 = 25$,解得$x=3$($x=4$舍),则BC=6,AD=4。
作点C关于AD的对称点B,连接BE交AD于F,则CF=BF,CF+EF=BF+EF=BE。
当BE⊥AC时,BE最小。
由S△ABC=$\frac{1}{2} × AC × BE=12$,得$\frac{1}{2} × 5 × BE=12 \Rightarrow BE=\frac{24}{5}$。
故CF+EF的最小值为$\frac{24}{5}$。
答案:D
4. 如图,等边三角形ABC的边长为$5,A,B,A_1$三点在同一条直线上,且$△ABC≌△A_1BC_1.$若D为线段$BC_1$上一动点,则AD+CD的最小值是____
10
.答案:10
解析:
解:∵△ABC≌△A₁BC₁,△ABC是等边三角形,边长为5,
∴BC=BA₁=5,∠ABC=∠A₁BC₁=60°,
∴∠CBC₁=180°-∠ABC-∠A₁BC₁=60°,
∴△CBC₁是等边三角形,
∴点C关于BC₁的对称点为A₁(或证明AC₁=10,利用两点之间线段最短),
∴AD+CD的最小值为AA₁=AB+BA₁=5+5=10。
10
∴BC=BA₁=5,∠ABC=∠A₁BC₁=60°,
∴∠CBC₁=180°-∠ABC-∠A₁BC₁=60°,
∴△CBC₁是等边三角形,
∴点C关于BC₁的对称点为A₁(或证明AC₁=10,利用两点之间线段最短),
∴AD+CD的最小值为AA₁=AB+BA₁=5+5=10。
10