8.(2024·泗洪期末)一个正方体的表面展开图如图所示,把它折成正方体后,与“要”相对的字是 (
A.细
B.心
C.检
D.查
D
)A.细
B.心
C.检
D.查
答案:D
9.将“科技、自立、自强”六个字分别写在某个正方体的表面上,如图是它的一种表面展开图,在原正方体中,与“强”字所在面相对面上的汉字是 (
A.自
B.立
C.科
D.技
C
)A.自
B.立
C.科
D.技
答案:C
解析:
在正方体表面展开图中,相对的面之间一定相隔一个正方形。
观察展开图:“科”与“强”相隔一个正方形,故“强”字所在面相对面上的汉字是“科”。
C
观察展开图:“科”与“强”相隔一个正方形,故“强”字所在面相对面上的汉字是“科”。
C
10.如图所示的图形是一些几何体的平面展开图,写出这些几何体的名称.
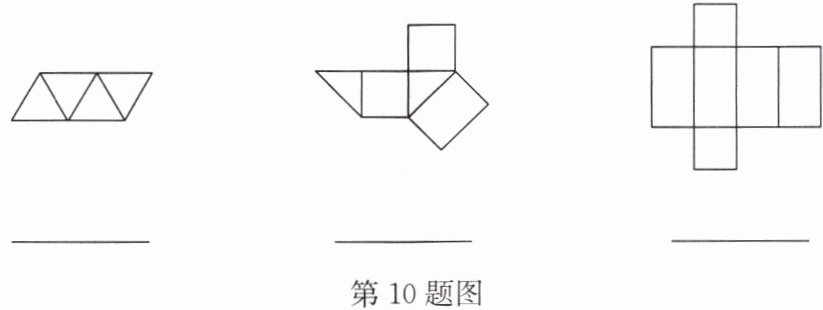

三棱锥
三棱柱
长方体
答案:三棱锥 三棱柱 长方体
11.如图是一个食品包装盒的表面展开图,其中长方形ABCD的周长为180cm,AD比AB长10cm.
(1)这个包装盒的形状是
(2)求这个包装盒的侧面积.

(1)这个包装盒的形状是
六棱柱
;(2)求这个包装盒的侧面积.

(2)解:设六棱柱侧面的每一个小长方形的长为x cm,则其宽为$\frac{90 - x}{4}$cm,根据题意,得90 - x = x - 10,解得x = 50,所以每一个小长方形的长为50 cm,宽为10 cm,故这个包装盒的侧面积为6×50×10 = 3000(cm²).答:这个包装盒的侧面积为3000 cm².
答案:
(1)六棱柱
(2)解:设六棱柱侧面的每一个小长方形的长为x cm,则其宽为$\frac{90 - x}{4}$cm,根据题意,得90 - x = x - 10,解得x = 50,所以每一个小长方形的长为50 cm,宽为10 cm,故这个包装盒的侧面积为6×50×10 = 3000(cm²).答:这个包装盒的侧面积为3000 cm².
(1)六棱柱
(2)解:设六棱柱侧面的每一个小长方形的长为x cm,则其宽为$\frac{90 - x}{4}$cm,根据题意,得90 - x = x - 10,解得x = 50,所以每一个小长方形的长为50 cm,宽为10 cm,故这个包装盒的侧面积为6×50×10 = 3000(cm²).答:这个包装盒的侧面积为3000 cm².
12.如图,在一个5×5的正方形网格中有五个小正方形,每个小正方形上分别标有一个数值,在网格中添上一个正方形,使之能折叠成一个正方体,且使所有相对面上的两个数值之和相等.
(1)在图中画出添上的正方形;(要求:在网格中用阴影形式描出,并描出所有符合条件的正方形)
(2)求添上的正方形上的数值.

(1)在图中画出添上的正方形;(要求:在网格中用阴影形式描出,并描出所有符合条件的正方形)
(2)求添上的正方形上的数值.

答案:
解:
(1)如答图所示.
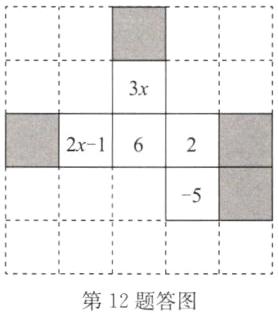
(2)设添加的正方形上的数值为y,根据题意,得3x - 5 = 2x - 1 + 2 = y + 6,解得x = 6,y = 7,故添上的正方形上的数值为7.
解:
(1)如答图所示.

(2)设添加的正方形上的数值为y,根据题意,得3x - 5 = 2x - 1 + 2 = y + 6,解得x = 6,y = 7,故添上的正方形上的数值为7.