4. 如图,在四边形$ABCD$中,$∠A+∠ABC+∠C+∠ADC= 360^{\circ}$,$∠A= ∠C= 90^{\circ}$,$∠ABC$,$∠ADC的平分线分别与AD$,$BC相交于点E$,$F$,$FG⊥BE于点G$,$∠1与∠2$之间有怎样的数量关系?请说明理由。
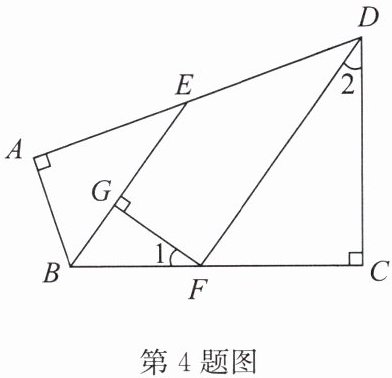

答案:解:∠1=∠2,理由如下:
因为∠A+∠ABC+∠C+∠ADC=360°,∠A=∠C=90°,
所以∠ABC+∠ADC=180°.
因为BE,DF分别平分∠ABC,∠ADC,
所以∠EBF=$\frac{1}{2}$∠ABC,∠2=$\frac{1}{2}$∠ADC,
所以∠EBF+∠2=90°.
因为FG⊥BE,
所以∠EBF+∠1=90°,所以∠1=∠2.
因为∠A+∠ABC+∠C+∠ADC=360°,∠A=∠C=90°,
所以∠ABC+∠ADC=180°.
因为BE,DF分别平分∠ABC,∠ADC,
所以∠EBF=$\frac{1}{2}$∠ABC,∠2=$\frac{1}{2}$∠ADC,
所以∠EBF+∠2=90°.
因为FG⊥BE,
所以∠EBF+∠1=90°,所以∠1=∠2.
5. 如图,直线$EF// GH$,点$A在EF$上,$AC交GH于点B$。若$∠EAB= 108^{\circ}$,点$D在GH$上,$∠BDC= 60^{\circ}$,求$∠ACD$的度数。


答案:解:因为EF//GH,
所以∠GBC=∠EAB=108°,
所以∠CBD=180°−∠GBC=180°−108°=72°.
因为∠BDC=60°,所以∠ACD=180°−∠CBD−∠BDC=180°−72°−60°=48°.
所以∠GBC=∠EAB=108°,
所以∠CBD=180°−∠GBC=180°−108°=72°.
因为∠BDC=60°,所以∠ACD=180°−∠CBD−∠BDC=180°−72°−60°=48°.
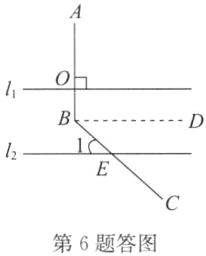
6. 如图,直线$l_{1}// l_{2}$,$AB⊥l_{1}$,垂足为$O$,$BC与l_{2}相交于点E$。若$∠1= 41^{\circ}$,求$∠ABC$的度数。


答案:
解:如答图,过点B作BD//l₁,
因为AB⊥l₁,
所以AB⊥BD,∠ABD=90°.
因为l₁//l₂,BD//l₁,
所以BD//l₂,
所以∠CBD=∠1=41°,
所以∠ABC=∠CBD+∠ABD=41°+90°=131°.
解:如答图,过点B作BD//l₁,
因为AB⊥l₁,
所以AB⊥BD,∠ABD=90°.
因为l₁//l₂,BD//l₁,
所以BD//l₂,
所以∠CBD=∠1=41°,
所以∠ABC=∠CBD+∠ABD=41°+90°=131°.
