1.(2024·兰州改编)-2024的绝对值的倒数是 (
A.2024
B.-2024
C.$\frac{1}{2024}$
D.$-\frac{1}{2024}$
C
)A.2024
B.-2024
C.$\frac{1}{2024}$
D.$-\frac{1}{2024}$
答案:C
解析:
$-2024$的绝对值是$|-2024| = 2024$,$2024$的倒数是$\frac{1}{2024}$,故选C。
2.(2024·潍坊)2024年3月份,低空经济首次被写入《政府工作报告》。截至2023年底,全国注册通航企业690家、无人机126.7万架,运营无人机的企业达1.9万家。将126.7万用科学记数法表示为 (
A.$1.267×10^{5}$
B.$1.267×10^{6}$
C.$1.267×10^{7}$
D.$126.7×10^{4}$
B
)A.$1.267×10^{5}$
B.$1.267×10^{6}$
C.$1.267×10^{7}$
D.$126.7×10^{4}$
答案:B
解析:
126.7万=1267000=1.267×10^{6}
B
B
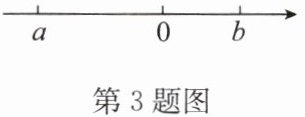
3.(2024·宿城期中)已知有理数a,b在数轴上对应点的位置如图所示,则下列式子错误的是 (
A.$a + b < 0$
B.$\frac{a}{b} < 0$
C.$|a| > |b|$
D.$-a < b$
D
)
A.$a + b < 0$
B.$\frac{a}{b} < 0$
C.$|a| > |b|$
D.$-a < b$
答案:D
解析:
由数轴可知,$a < 0 < b$,且$|a| > |b|$。
A. $a + b < 0$,正确;
B. $\frac{a}{b} < 0$,正确;
C. $|a| > |b|$,正确;
D. $-a > b$,错误。
D
A. $a + b < 0$,正确;
B. $\frac{a}{b} < 0$,正确;
C. $|a| > |b|$,正确;
D. $-a > b$,错误。
D
4. 计算$-1^{2024} + (-2)^{3} + 2×(-3)$的结果为 (
A.-13
B.-14
C.-15
D.-16
C
)A.-13
B.-14
C.-15
D.-16
答案:C
解析:
$-1^{2024} + (-2)^{3} + 2×(-3)$
$=-1 + (-8) + (-6)$
$=-1 - 8 - 6$
$=-15$
C
$=-1 + (-8) + (-6)$
$=-1 - 8 - 6$
$=-15$
C
5. 在解决数学实际问题时,常常用到数形结合思想,比如:$|x + 1|$的几何意义是数轴上表示数x的点与表示数-1的点的距离。当$|x + 1| + |x - 2|$取得最小值时,x的取值范围是 (
A.$x ≤ -1$
B.$x ≤ -1或x ≥ 2$
C.$-1 ≤ x ≤ 2$
D.$x ≥ 2$
C
)A.$x ≤ -1$
B.$x ≤ -1或x ≥ 2$
C.$-1 ≤ x ≤ 2$
D.$x ≥ 2$
答案:C
解析:
$|x + 1|$的几何意义是数轴上表示数$x$的点与表示数$-1$的点的距离,$|x - 2|$的几何意义是数轴上表示数$x$的点与表示数$2$的点的距离。当表示数$x$的点在表示$-1$和$2$的两点之间(包括这两点)时,$|x + 1| + |x - 2|$的值为这两点之间的距离,即$2 - (-1) = 3$,此时取得最小值。当$x < -1$或$x > 2$时,$|x + 1| + |x - 2|$的值大于$3$。所以当$|x + 1| + |x - 2|$取得最小值时,$x$的取值范围是$-1 ≤ x ≤ 2$。
C
C
6.(2024·宿豫期末)超市销售一种精制面粉,袋上标明质量为$5_{-0.03}^{+0.03}$千克,如果某袋面粉重5.02千克,那么它的质量
符合
标准。(填“符合”或“不符合”)答案:符合
7.(2024·江西改编)计算:$-2^{4} - (-1)^{3} = $
-15
。答案:-15
解析:
$-2^{4} - (-1)^{3} = -16 - (-1) = -16 + 1 = -15$
8. 有理数-4,500,0,-2.67,$5\frac{3}{4}$中,整数是
-4,500,0
,负整数是-4
,正分数是$5\frac{3}{4}$
。答案:-4,500,0 -4 $5\frac{3}{4}$
9.(2024·宿城期中)已知纸面上有一数轴,折叠纸面,使表示-3的点与表示1的点重合,则表示-20的点与表示
18
的点重合。答案:18
解析:
-3与1的中点为$\frac{-3 + 1}{2}=-1$。设与-20重合的点为$x$,则$\frac{-20 + x}{2}=-1$,解得$x = 18$。18
10.(2024·宿迁新区共同体期末)若一列数$a_{1}$,$a_{2}$,$a_{3}$,$a_{4}$,…中的任意三个相邻数之和都是40,已知$a_{3} = 3m$,$a_{20} = 16$,$a_{99} = 12 - m$,则$a_{2024} = $
16
。答案:16
解析:
由题意得$a_{1}+a_{2}+a_{3}=40$,$a_{2}+a_{3}+a_{4}=40$,则$a_{1}=a_{4}$;同理可得$a_{2}=a_{5}$,$a_{3}=a_{6}$,所以数列周期为3。
因为$20÷3=6\cdots\cdots2$,所以$a_{20}=a_{2}=16$;$99÷3=33$,所以$a_{99}=a_{3}=12 - m$,又$a_{3}=3m$,故$3m=12 - m$,解得$m=3$,则$a_{3}=9$。
由$a_{1}+a_{2}+a_{3}=40$,得$a_{1}=40 - a_{2}-a_{3}=40 - 16 - 9=15$。
$2024÷3=674\cdots\cdots2$,所以$a_{2024}=a_{2}=16$。
16
因为$20÷3=6\cdots\cdots2$,所以$a_{20}=a_{2}=16$;$99÷3=33$,所以$a_{99}=a_{3}=12 - m$,又$a_{3}=3m$,故$3m=12 - m$,解得$m=3$,则$a_{3}=9$。
由$a_{1}+a_{2}+a_{3}=40$,得$a_{1}=40 - a_{2}-a_{3}=40 - 16 - 9=15$。
$2024÷3=674\cdots\cdots2$,所以$a_{2024}=a_{2}=16$。
16