9. (2024·江都区期末)一个n棱柱有18条棱,底面每条边的长都是5cm,那么它的下底面周长是
30
cm.答案:30
解析:
一个n棱柱有3n条棱,由题意得3n=18,解得n=6。所以该棱柱为六棱柱,下底面是六边形,底面每条边的长都是5cm,下底面周长为6×5=30cm。
30
30
10. (2024·贾汪区期末)七巧板被西方人称为“东方魔术”,如图所示的两幅图是由同一个七巧板拼成的,左侧大正方形的边长为4,则右侧阴影部分的面积是______
8
.答案:8
解析:
左侧大正方形边长为4,面积为$4^2 = 16$。
七巧板由5个等腰直角三角形(2大、1中、2小)、1个正方形和1个平行四边形组成。设小等腰直角三角形直角边为$a$,则中三角形直角边为$\sqrt{2}a$,大三角形直角边为$2a$,正方形边长为$a$,平行四边形边长为$a$和$\sqrt{2}a$。
大正方形边长由2个大三角形直角边组成,即$2a + 2a = 4$(或根据七巧板拼接关系,大正方形边长为$2\sqrt{2}a$,解得$a = \sqrt{2}$)。
右侧阴影部分由2个大等腰直角三角形组成,每个大三角形面积为$\frac{1}{2} × (2a)^2 = 2a^2$,2个面积为$4a^2$。由大正方形面积$16 = 8a^2$(七巧板总面积等于大正方形面积,8个小三角形面积和为$8 × \frac{1}{2}a^2 = 4a^2$,此处应为七巧板面积组成:2大(各2小三角形面积)、1中(1小)、2小(各1小)、1正方形(1小)、1平行四边形(1小),共$2×2 + 1 + 2 + 1 + 1 = 8$小三角形面积,即$8 × \frac{1}{2}a^2 = 4a^2 = 16$,得$a^2 = 4$),则阴影面积$4a^2 = 8$。
8
七巧板由5个等腰直角三角形(2大、1中、2小)、1个正方形和1个平行四边形组成。设小等腰直角三角形直角边为$a$,则中三角形直角边为$\sqrt{2}a$,大三角形直角边为$2a$,正方形边长为$a$,平行四边形边长为$a$和$\sqrt{2}a$。
大正方形边长由2个大三角形直角边组成,即$2a + 2a = 4$(或根据七巧板拼接关系,大正方形边长为$2\sqrt{2}a$,解得$a = \sqrt{2}$)。
右侧阴影部分由2个大等腰直角三角形组成,每个大三角形面积为$\frac{1}{2} × (2a)^2 = 2a^2$,2个面积为$4a^2$。由大正方形面积$16 = 8a^2$(七巧板总面积等于大正方形面积,8个小三角形面积和为$8 × \frac{1}{2}a^2 = 4a^2$,此处应为七巧板面积组成:2大(各2小三角形面积)、1中(1小)、2小(各1小)、1正方形(1小)、1平行四边形(1小),共$2×2 + 1 + 2 + 1 + 1 = 8$小三角形面积,即$8 × \frac{1}{2}a^2 = 4a^2 = 16$,得$a^2 = 4$),则阴影面积$4a^2 = 8$。
8
11. (2024·滨湖区期末)有下面四种现象:①旋转一扇门,门运动的痕迹;②扔一块小石子,石子在空中飞行的路线;③夜晚天空划过流星的痕迹;④汽车雨刷在挡风玻璃上画出的痕迹.其中能说明“线动成面”的现象是______.(填序号)
④
答案:④
12. 如图所示的图形能围成的立体图形是
四棱锥
.答案:四棱锥
13. (2024·玄武区期末)如图所示的图形中为柱体的是
②③
,其中为圆柱的是②
,为棱柱的是③
.(填序号)答案:②③ ② ③
14. 若一个直棱柱有12个顶点,且所有侧棱长的和为54cm,则每条侧棱长为
9
cm.答案:9
解析:
直棱柱顶点个数为12,因为直棱柱顶点个数=2×底面边数,所以底面边数为12÷2=6,即该直棱柱为六棱柱,有6条侧棱。所有侧棱长的和为54cm,每条侧棱长为54÷6=9cm。
9
9
15. 如图是同一个标有1,2,3,4,5,6的小正方体的三种不同的摆法.图中三个正方体朝左的一面的数字之积是______
20
.答案:20
解析:
由图①②可知,与3相邻的数字为1、2、4,故3的对面是5;由图①③可知,与1相邻的数字为2、3、6,故1的对面是4;则2的对面是6。
图①朝左一面数字为5,图②朝左一面数字为1,图③朝左一面数字为2。
三个数字之积为 $5×1×2=10$。
1
图①朝左一面数字为5,图②朝左一面数字为1,图③朝左一面数字为2。
三个数字之积为 $5×1×2=10$。
1
16. 一个圆柱的侧面展开图如图所示,则其底面圆的面积为
4π或π
.答案:4π或π
解析:
- 情况一:圆柱底面周长为$4\pi$,则底面半径$r = \frac{4\pi}{2\pi} = 2$,底面圆面积为$\pi r^2 = \pi × 2^2 = 4\pi$
情况二:圆柱底面周长为$2\pi$,则底面半径$r = \frac{2\pi}{2\pi} = 1$,底面圆面积为$\pi r^2 = \pi × 1^2 = \pi$
4π或π
情况二:圆柱底面周长为$2\pi$,则底面半径$r = \frac{2\pi}{2\pi} = 1$,底面圆面积为$\pi r^2 = \pi × 1^2 = \pi$
4π或π
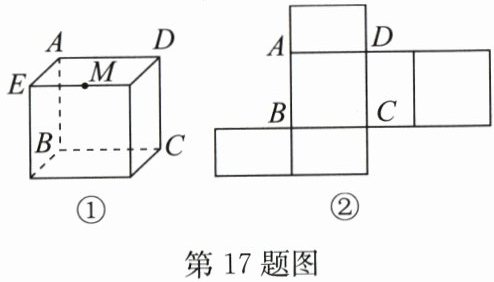
17. (2024·鼓楼区期末)如图,图①为一个长方体,AD= AB= 8,AE= 5,M为所在棱的中点,图②为图①的表面展开图,则图②中三角形ABM的面积为$
68或16
cm^2.$
答案:68或16