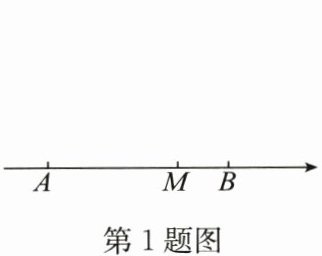
1.(2024·赤峰)如图,数轴上点A,M,B分别表示数a,$a + b$,b.若$AM>BM$,则下列运算结果一定是正数的是 (
A.$a + b$
B.$a - b$
C.ab
D.$|a| - b$
A
)
A.$a + b$
B.$a - b$
C.ab
D.$|a| - b$
答案:A
解析:
由数轴可知点A、M、B的位置顺序为A<M<B,即$a < a + b < b$。
由$a < a + b$可得$b > 0$;由$a + b < b$可得$a < 0$。
$AM = (a + b) - a = b$,$BM = b - (a + b) = -a$,因为$AM > BM$,所以$b > -a$,即$a + b > 0$。
A选项:$a + b > 0$,结果为正数;
B选项:$a - b$,$a < 0$,$b > 0$,则$a - b < 0$;
C选项:$ab$,$a < 0$,$b > 0$,则$ab < 0$;
D选项:$|a| - b$,$|a| = -a$,由$b > -a$可得$|a| - b = -a - b < 0$。
综上,运算结果一定是正数的是A选项。
A
由$a < a + b$可得$b > 0$;由$a + b < b$可得$a < 0$。
$AM = (a + b) - a = b$,$BM = b - (a + b) = -a$,因为$AM > BM$,所以$b > -a$,即$a + b > 0$。
A选项:$a + b > 0$,结果为正数;
B选项:$a - b$,$a < 0$,$b > 0$,则$a - b < 0$;
C选项:$ab$,$a < 0$,$b > 0$,则$ab < 0$;
D选项:$|a| - b$,$|a| = -a$,由$b > -a$可得$|a| - b = -a - b < 0$。
综上,运算结果一定是正数的是A选项。
A
2.(2024·宿城期中)如图,点E在BC的延长线上,下列条件中,不能推断$AB// CD$的是 (

A.$∠4 = ∠3$
B.$∠1 = ∠2$
C.$∠B = ∠5$
D.$∠B + ∠BCD = 180^{\circ}$
A
)
A.$∠4 = ∠3$
B.$∠1 = ∠2$
C.$∠B = ∠5$
D.$∠B + ∠BCD = 180^{\circ}$
答案:A
3.(2024·达州)如图,正方体的表面展开图上写有“我们热爱中国”六个字,还原成正方体后“我”的对面的字是 (
A.热
B.爱
C.中
D.国
B
)A.热
B.爱
C.中
D.国
答案:B
解析:
将展开图还原成正方体,“我”与“爱”相对。
B
B
4.现有一列火车匀速从桥上通过,测得火车从开始上桥到完全通过共用70秒,整列火车完全在桥上的时间是55秒,火车的长度为200米,若设该桥的长度为x米,则所列方程正确的是 (
A.$\frac{x + 200}{55} = \frac{x - 200}{70}$
B.$\frac{x}{55} = \frac{x + 200}{70}$
C.$\frac{x - 200}{55} = \frac{x + 200}{70}$
D.$\frac{x + 200}{55} = \frac{x}{70}$
C
)A.$\frac{x + 200}{55} = \frac{x - 200}{70}$
B.$\frac{x}{55} = \frac{x + 200}{70}$
C.$\frac{x - 200}{55} = \frac{x + 200}{70}$
D.$\frac{x + 200}{55} = \frac{x}{70}$
答案:C
解析:
火车从开始上桥到完全通过所行驶的路程为桥长与火车长之和,即$(x + 200)$米,共用70秒,所以火车速度为$\frac{x + 200}{70}$米/秒;整列火车完全在桥上所行驶的路程为桥长与火车长之差,即$(x - 200)$米,时间是55秒,所以火车速度为$\frac{x - 200}{55}$米/秒。由于火车匀速行驶,速度相等,故所列方程为$\frac{x - 200}{55} = \frac{x + 200}{70}$。
C
C
5.如图,直线AB,CD相交于点O,$OE⊥AB$,垂足为O,OF平分$∠BOD$.若$∠AOC + ∠DOF = 39^{\circ}$,则$∠EOF$的度数为 (
A.$77^{\circ}$
B.$74^{\circ}$
C.$67^{\circ}$
D.$64^{\circ}$
A
)A.$77^{\circ}$
B.$74^{\circ}$
C.$67^{\circ}$
D.$64^{\circ}$
答案:A
解析:
∵直线AB,CD相交于点O,
∴∠AOC=∠BOD(对顶角相等)。
∵OF平分∠BOD,
∴∠DOF=∠BOF=$\frac{1}{2}$∠BOD=$\frac{1}{2}$∠AOC。
设∠AOC=x,则∠DOF=$\frac{1}{2}$x。
∵∠AOC + ∠DOF = 39°,
∴x + $\frac{1}{2}$x = 39°,解得x=26°。
∴∠BOD=26°,∠BOF=$\frac{1}{2}$×26°=13°。
∵OE⊥AB,
∴∠EOB=90°。
∴∠EOF=∠EOB + ∠BOF=90° + 13°=103°。
1
∴∠AOC=∠BOD(对顶角相等)。
∵OF平分∠BOD,
∴∠DOF=∠BOF=$\frac{1}{2}$∠BOD=$\frac{1}{2}$∠AOC。
设∠AOC=x,则∠DOF=$\frac{1}{2}$x。
∵∠AOC + ∠DOF = 39°,
∴x + $\frac{1}{2}$x = 39°,解得x=26°。
∴∠BOD=26°,∠BOF=$\frac{1}{2}$×26°=13°。
∵OE⊥AB,
∴∠EOB=90°。
∴∠EOF=∠EOB + ∠BOF=90° + 13°=103°。
1
6.(2024·无锡经开区期末)如图,$CD = \frac{1}{4}AD = \frac{1}{5}BC$,E,F分别是AC,BC的中点,且$BF = 20cm$,则EF的长度为
32
cm.答案:32
解析:
∵F是BC的中点,BF=20cm,
∴BC=2BF=40cm。
∵CD=$\frac{1}{5}$BC,
∴CD=$\frac{1}{5}×40=8$cm。
∵CD=$\frac{1}{4}$AD,
∴AD=4CD=32cm。
∵AD=AC+CD,
∴AC=AD-CD=32-8=24cm。
∵E是AC的中点,
∴CE=$\frac{1}{2}$AC=12cm。
∵F是BC的中点,
∴CF=BF=20cm。
∵EF=CE+CF,
∴EF=12+20=32cm。
32
∴BC=2BF=40cm。
∵CD=$\frac{1}{5}$BC,
∴CD=$\frac{1}{5}×40=8$cm。
∵CD=$\frac{1}{4}$AD,
∴AD=4CD=32cm。
∵AD=AC+CD,
∴AC=AD-CD=32-8=24cm。
∵E是AC的中点,
∴CE=$\frac{1}{2}$AC=12cm。
∵F是BC的中点,
∴CF=BF=20cm。
∵EF=CE+CF,
∴EF=12+20=32cm。
32
7.如图,一束光线从点C出发,经过平面镜AB反射后,沿与AF平行的射线DE射出(此时$∠1 = ∠2$).若测得$∠DCF = 100^{\circ}$,则$∠A = $
50°
.答案:50°
解析:
∵DE//AF,
∴∠2=∠A。
∵∠1=∠2,
∴∠1=∠A。
∵∠DCF=100°,∠DCF+∠ACD=180°,
∴∠ACD=180°-100°=80°。
∵∠A+∠1+∠ACD=180°,∠1=∠A,
∴2∠A+80°=180°,
∴∠A=50°。
50°
∴∠2=∠A。
∵∠1=∠2,
∴∠1=∠A。
∵∠DCF=100°,∠DCF+∠ACD=180°,
∴∠ACD=180°-100°=80°。
∵∠A+∠1+∠ACD=180°,∠1=∠A,
∴2∠A+80°=180°,
∴∠A=50°。
50°