1. 两条直线相交所成的四个角中,有公共
2. 对顶角的性质:两直线相交,对顶角
顶点
没有公共边
的两个角叫作对顶角.2. 对顶角的性质:两直线相交,对顶角
相等
.答案:1. 顶点 边 2. 相等
1. 如图,$∠1与∠2$是对顶角的图形有 (
A.0个
B.1个
C.2个
D.3个
C
)A.0个
B.1个
C.2个
D.3个
答案:C
解析:
对顶角的定义:两条直线相交后所得的只有一个公共顶点且两边互为反向延长线的两个角叫做对顶角。
分析各图形:
图①:∠1与∠2没有公共顶点,不是对顶角。
图②:∠1与∠2的两边不互为反向延长线,不是对顶角。
图③:∠1与∠2有公共顶点,且两边互为反向延长线,是对顶角。
图④:∠1与∠2的两边不互为反向延长线,不是对顶角。
图⑤:∠1与∠2有公共顶点,且两边互为反向延长线,是对顶角。
综上,是对顶角的图形有2个。
C
分析各图形:
图①:∠1与∠2没有公共顶点,不是对顶角。
图②:∠1与∠2的两边不互为反向延长线,不是对顶角。
图③:∠1与∠2有公共顶点,且两边互为反向延长线,是对顶角。
图④:∠1与∠2的两边不互为反向延长线,不是对顶角。
图⑤:∠1与∠2有公共顶点,且两边互为反向延长线,是对顶角。
综上,是对顶角的图形有2个。
C
2. 如图,若$∠1= ∠2$,则与$∠3$相等的角有 (
A.1个
B.2个
C.3个
D.4个
C
)A.1个
B.2个
C.3个
D.4个
答案:C
解析:
解:由图可知,∠1与∠2是同位角,因为∠1=∠2,所以两直线平行。
两直线平行,同位角相等,内错角相等。
∠3的对顶角与∠3相等;
∠3的同位角(与∠1位置相同的角)与∠3相等;
∠3的内错角(与∠2位置相对的角)与∠3相等。
所以与∠3相等的角有3个。
答案:C
两直线平行,同位角相等,内错角相等。
∠3的对顶角与∠3相等;
∠3的同位角(与∠1位置相同的角)与∠3相等;
∠3的内错角(与∠2位置相对的角)与∠3相等。
所以与∠3相等的角有3个。
答案:C
3. 如图,直线AB,CD相交于点O,若$∠1+∠2= 52^{\circ }$,则$∠AOC= $
154°
.答案:154°
解析:
解:由对顶角相等,得∠1=∠2。
因为∠1+∠2=52°,所以∠1=∠2=26°。
∠AOC与∠1互为邻补角,故∠AOC=180°-∠1=180°-26°=154°。
154°
因为∠1+∠2=52°,所以∠1=∠2=26°。
∠AOC与∠1互为邻补角,故∠AOC=180°-∠1=180°-26°=154°。
154°
4. 如图,直线AB与CD相交所成的四个角中,$∠1$的对顶角是
∠3
.答案:∠3
5. 如图,若$∠1= 25^{\circ }$,则$∠2= $
155°
,$∠3= $25°
,$∠4= $155°
.答案:155° 25° 155°
解析:
解:
由图可知,∠1与∠2互为邻补角,
∠2 = 180° - ∠1 = 180° - 25° = 155°;
∠1与∠3是对顶角,
∠3 = ∠1 = 25°;
∠2与∠4是对顶角,
∠4 = ∠2 = 155°。
∠2=155°,∠3=25°,∠4=155°
由图可知,∠1与∠2互为邻补角,
∠2 = 180° - ∠1 = 180° - 25° = 155°;
∠1与∠3是对顶角,
∠3 = ∠1 = 25°;
∠2与∠4是对顶角,
∠4 = ∠2 = 155°。
∠2=155°,∠3=25°,∠4=155°
6. 已知$∠1= 60^{\circ },∠1与∠2$是邻补角,$∠1与∠3$是对顶角,则$∠2= $
120°
,$∠3= $60°
.答案:120° 60°
解析:
解:因为∠1与∠2是邻补角,邻补角之和为180°,∠1=60°,所以∠2=180° - ∠1=180° - 60°=120°。
因为∠1与∠3是对顶角,对顶角相等,∠1=60°,所以∠3=∠1=60°。
∠2=120°,∠3=60°
因为∠1与∠3是对顶角,对顶角相等,∠1=60°,所以∠3=∠1=60°。
∠2=120°,∠3=60°
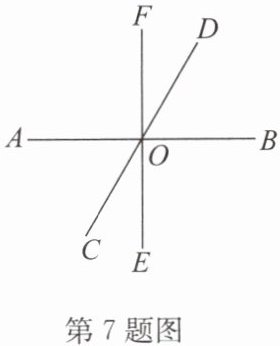
7. 如图,直线AB,CD,EF相交于点O.
(1)写出$∠COE$的邻补角;
(2)分别写出$∠COE和∠BOE$的对顶角;
(3)如果$∠BOD= 60^{\circ },∠BOF= 90^{\circ }$,求$∠AOF和∠FOC$的度数.
(1)写出$∠COE$的邻补角;
(2)分别写出$∠COE和∠BOE$的对顶角;
(3)如果$∠BOD= 60^{\circ },∠BOF= 90^{\circ }$,求$∠AOF和∠FOC$的度数.

答案:解:(1)∠COE 的邻补角为∠COF 和∠EOD.
(2)∠COE 的对顶角为∠DOF,∠BOE 的对顶角为∠AOF.
(3)∠AOF=180°-∠BOF=180°-90°=90°.
因为∠BOF=90°,∠BOD=60°,
所以∠FOD=∠BOF-∠BOD=90°-60°=30°,
所以∠FOC=180°-∠FOD=180°-30°=150°.
(2)∠COE 的对顶角为∠DOF,∠BOE 的对顶角为∠AOF.
(3)∠AOF=180°-∠BOF=180°-90°=90°.
因为∠BOF=90°,∠BOD=60°,
所以∠FOD=∠BOF-∠BOD=90°-60°=30°,
所以∠FOC=180°-∠FOD=180°-30°=150°.