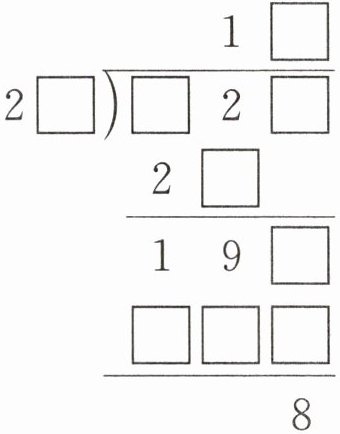
例 选择合适的数字填在□里,使下面的算式成立。
解析
抓住被除数前两位够除,商的十位上是1这个突破口来考虑。根据被除数十位上是2和余数是19可知,除数个位上的数字3,即除数是23。据此又可推断出被除数百位上的数字为4。23×7= 161,23×8= 184,23×9= 207,结合最后的余数是8,可以推出商是18。
答案:
小结
解决除法算式谜问题的关键:分析竖式的结构特征,找出已给的数字之间的关系,选择解题突破口,找出关键数字的范围,逐一检验。

解析
抓住被除数前两位够除,商的十位上是1这个突破口来考虑。根据被除数十位上是2和余数是19可知,除数个位上的数字3,即除数是23。据此又可推断出被除数百位上的数字为4。23×7= 161,23×8= 184,23×9= 207,结合最后的余数是8,可以推出商是18。
答案:
$\begin{array}{r r r r r r r r r }&&&&1&8 \\ \hline &2&3)&4&2&2 \\ &&&2&3 \\ \hline &&&1&9&2 \\ &&&1&8&4 \\ \hline &&&&&8\end{array}$
小结
解决除法算式谜问题的关键:分析竖式的结构特征,找出已给的数字之间的关系,选择解题突破口,找出关键数字的范围,逐一检验。
答案:解析:
抓住被除数前两位够除,商的十位上是$1$这个突破口来考虑。根据被除数十位上是$2$和余数是$19$可知,除数个位上的数字$3$,即除数是$23$。据此又可推断出被除数百位上的数字为$4$。
$23×7= 161$,$23×8=184$,$23×9=207$,结合最后的余数是$8$,可以推出商是$18$。
答案:
$\begin{array}{r r r r r r r r r }&&&&1&8 \\ \hline &2&3)&4&2&2 \\ &&&2&3 \\ \hline &&&1&9&2 \\ &&&1&8&4 \\ \hline &&&&&8\end{array}$
抓住被除数前两位够除,商的十位上是$1$这个突破口来考虑。根据被除数十位上是$2$和余数是$19$可知,除数个位上的数字$3$,即除数是$23$。据此又可推断出被除数百位上的数字为$4$。
$23×7= 161$,$23×8=184$,$23×9=207$,结合最后的余数是$8$,可以推出商是$18$。
答案:
$\begin{array}{r r r r r r r r r }&&&&1&8 \\ \hline &2&3)&4&2&2 \\ &&&2&3 \\ \hline &&&1&9&2 \\ &&&1&8&4 \\ \hline &&&&&8\end{array}$
1. 下面竖式中,被除数+除数+商+余数=430,在□里填合适的数字。


答案:
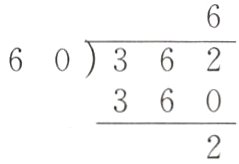
[提示]由题意可知,从430里去掉除数与余数的和,剩下的是商和被除数的和,而被除数是商的60倍还多2,把商看作1份,则(430 - 60 - 2 - 2)对应的是1份加60份的总和,商是(430 - 60 - 2 - 2)÷(60 + 1)=6,被除数是60×6 + 2=362。因此除法算式是362÷60 = 6……2。
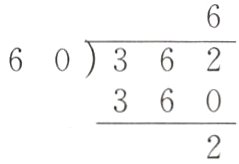
[提示]由题意可知,从430里去掉除数与余数的和,剩下的是商和被除数的和,而被除数是商的60倍还多2,把商看作1份,则(430 - 60 - 2 - 2)对应的是1份加60份的总和,商是(430 - 60 - 2 - 2)÷(60 + 1)=6,被除数是60×6 + 2=362。因此除法算式是362÷60 = 6……2。
2. 下面竖式中,相同的字母代表相同的数字,□里的数字可以相同也可以不同。下面竖式的商是(
83
)。答案:83 [提示]因为BA×A = 304,积的个位上是4,可得A只能是2或8,当A是2时,积不可能是304,因此A是8。进一步算出B是3。
3. 下面竖式中,相同的字母代表相同的数字,不同的字母代表不同的数字,求出它们使竖式成立的值。


答案:A = 1,B = 9,C = 3,D = 0,E = 2,F = 5,G = 4,H = 8,I = 7,J = 6。
[提示]被除数前三位除以除数后,余数是两位数,可以判断出被除数的最高位A = 1,进而可以判断出B = 9,即除数是19,再求出其他字母代表的数字即可。
[提示]被除数前三位除以除数后,余数是两位数,可以判断出被除数的最高位A = 1,进而可以判断出B = 9,即除数是19,再求出其他字母代表的数字即可。