1. 下面是某公司第一车间三个小组男、女工人数统计图,看图回答问题。
某公司第一车间三个小组男、女工人数统计图
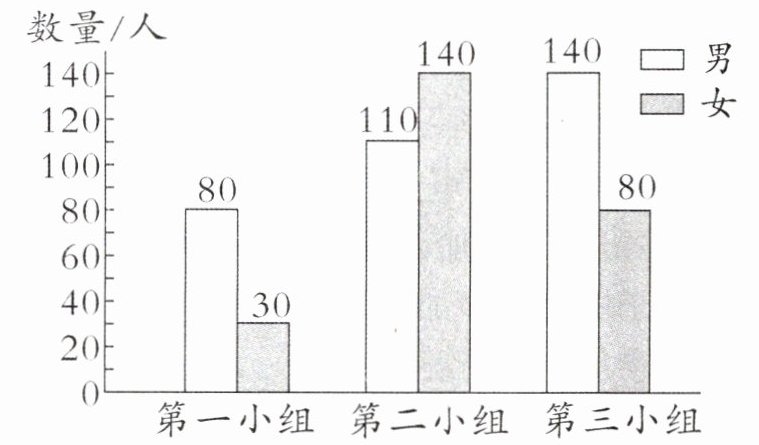
(1)男工人数最多的是第(
(2)第(
某公司第一车间三个小组男、女工人数统计图

(1)男工人数最多的是第(
三
)小组,最少的是第(一
)小组;女工人数最多的是第(二
)小组,最少的是第(一
)小组。(2)第(
二
)小组的工人人数最多,有(250
)人;第(一
)小组的工人人数最少,有(110
)人。答案:1.
(1)三 一 二 一 【提示】根据直条的高低来判断,直条越高,表示人数越多。
(2)二 250 一 110 【提示】根据直条上的数据来填写。
(1)三 一 二 一 【提示】根据直条的高低来判断,直条越高,表示人数越多。
(2)二 250 一 110 【提示】根据直条上的数据来填写。
2. 根据下图回答问题。
由污染造成的经济损失统计图

(1)水污染造成经济损失最多的省份是(
(2)大气污染造成经济损失最多的省份是(
(3)这四个省水污染造成经济损失共(
(4)江苏省的水污染比大气污染造成的经济损失多(
由污染造成的经济损失统计图

(1)水污染造成经济损失最多的省份是(
江苏
)。(2)大气污染造成经济损失最多的省份是(
云南
)。(3)这四个省水污染造成经济损失共(
635
)万元。(4)江苏省的水污染比大气污染造成的经济损失多(
291
)万元。答案:2.
(1)江苏
(2)云南
(3)635
(4)291
【提示】
(1)
(2)根据直条的高低填写,直条越高,代表污染造成的经济损失越多;
(3)327+129+69+110=635(万元);
(4)327-36=291(万元)。
(1)江苏
(2)云南
(3)635
(4)291
【提示】
(1)
(2)根据直条的高低填写,直条越高,代表污染造成的经济损失越多;
(3)327+129+69+110=635(万元);
(4)327-36=291(万元)。
3. 下面是五(3)班同学参加艺术节活动人数统计表。

(1)根据表中数据完成下面的统计图。
五(3)班同学参加艺术节活动人数统计图

(2)参加(
(3)这个班至少有(
(4)你想参加哪项活动,理由是什么?

(1)根据表中数据完成下面的统计图。
五(3)班同学参加艺术节活动人数统计图

(2)参加(
书法
)活动的人数最多,(跳舞
)活动的人数最少。(3)这个班至少有(
53
)人。(4)你想参加哪项活动,理由是什么?
答案不唯一,合理即可。
答案:
(1)如图所示
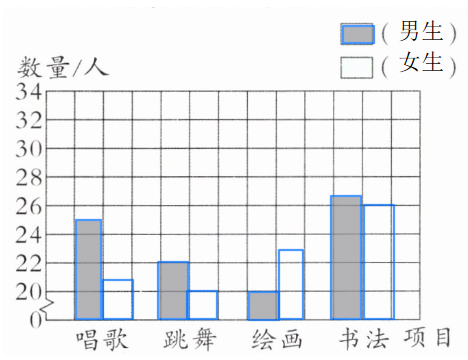
$(2)$
参加(书法)活动的人数最多,(跳舞)活动的人数最少。
$(3)$
解:要使班级人数最少,则让参加各项活动的人员重复最少。
参加唱歌的有$25 + 21=46$人;参加跳舞的有$22 + 20 = 42$人;参加绘画的有$20+23 = 43$人;参加书法的有$27+26 = 53$人。
因为$53\gt46\gt43\gt42$,所以这个班至少有$53$人。
$(4)$
示例:我想参加绘画活动,理由是绘画可以发挥我的想象力,用画笔描绘出美丽的世界。(答案不唯一,合理即可)
(1)如图所示

$(2)$
参加(书法)活动的人数最多,(跳舞)活动的人数最少。
$(3)$
解:要使班级人数最少,则让参加各项活动的人员重复最少。
参加唱歌的有$25 + 21=46$人;参加跳舞的有$22 + 20 = 42$人;参加绘画的有$20+23 = 43$人;参加书法的有$27+26 = 53$人。
因为$53\gt46\gt43\gt42$,所以这个班至少有$53$人。
$(4)$
示例:我想参加绘画活动,理由是绘画可以发挥我的想象力,用画笔描绘出美丽的世界。(答案不唯一,合理即可)
4.下面是五(1)班同学踢毽子测试等级的情
况。根据记录的数据,完成统计图,并回答
问题。


45
)人,获得(优秀
)等级的人数最多。(2)如果五年级一共有 360 人,根据这个班学生踢毽子测试的情况估计一下,整个五年级学生踢毽子成绩优秀的大约有多少人?在正确答案后面的方框里画“√”。
60 人□ 160 人☑ 220 人□
(3)请借助推理或计算,简要说明第(2)题的判断理由。
五(1)班踢毽子测试等级优秀的学生占全班总人数的$\frac{20}{45}$,据此可以推断出,整个五年级踢毽子等级优秀的学生占全年级总人数的$\frac{20}{45}$,可以估算出是160人。或者列式360÷45×20=160(人)。
答案:$(1)$ 计算五$(1)$班总人数并找出人数最多的等级
- 计算总人数:将各等级男女生人数相加,即$(8 + 12)+(7 + 6)+(6 + 4)+(1 + 1)$
$=20 + 13+10 + 2$
$=45$(人)。
- 计算各等级人数:
优秀:$8 + 12=20$(人);
良好:$7 + 6 = 13$(人);
合格:$6 + 4 = 10$(人);
不合格:$1 + 1 = 2$(人)。
比较可得$20\gt13\gt10\gt2$,获得优秀等级的人数最多。
$(2)$ 选择五年级优秀人数的估计值
五$(1)$班优秀人数为$20$人,总人数$45$人,五年级共$360$人。
五$(1)$班优秀人数占比为$\frac{20}{45}=\frac{4}{9}$,则五年级优秀人数大约为$360×\frac{4}{9}=160$(人),所以在$160$人后面的方框画“√”。
$(3)$ 说明判断理由
- 先算出五$(1)$班优秀人数占班级总人数的比例:
五$(1)$班优秀人数$8 + 12 = 20$人,班级总人数$45$人,优秀人数占比$=\frac{20}{45}=\frac{4}{9}$。
- 再根据比例计算五年级优秀人数:
五年级共$360$人,因为用五$(1)$班优秀人数占比来估计五年级优秀人数占比,所以五年级优秀人数大约为$360×\frac{4}{9}$
$=360÷9×4$
$ = 40×4$
$=160$人。
综上,答案依次为:$(1)$$\boldsymbol{45}$,优秀;$(2)$$\boldsymbol{160}$人$\boldsymbol{\surd}$ ;$(3)$ 先算五$(1)$班优秀人数占比$\frac{20}{45}=\frac{4}{9}$,再用五年级总人数$360$乘以该占比$360×\frac{4}{9}=160$人。
- 计算总人数:将各等级男女生人数相加,即$(8 + 12)+(7 + 6)+(6 + 4)+(1 + 1)$
$=20 + 13+10 + 2$
$=45$(人)。
- 计算各等级人数:
优秀:$8 + 12=20$(人);
良好:$7 + 6 = 13$(人);
合格:$6 + 4 = 10$(人);
不合格:$1 + 1 = 2$(人)。
比较可得$20\gt13\gt10\gt2$,获得优秀等级的人数最多。
$(2)$ 选择五年级优秀人数的估计值
五$(1)$班优秀人数为$20$人,总人数$45$人,五年级共$360$人。
五$(1)$班优秀人数占比为$\frac{20}{45}=\frac{4}{9}$,则五年级优秀人数大约为$360×\frac{4}{9}=160$(人),所以在$160$人后面的方框画“√”。
$(3)$ 说明判断理由
- 先算出五$(1)$班优秀人数占班级总人数的比例:
五$(1)$班优秀人数$8 + 12 = 20$人,班级总人数$45$人,优秀人数占比$=\frac{20}{45}=\frac{4}{9}$。
- 再根据比例计算五年级优秀人数:
五年级共$360$人,因为用五$(1)$班优秀人数占比来估计五年级优秀人数占比,所以五年级优秀人数大约为$360×\frac{4}{9}$
$=360÷9×4$
$ = 40×4$
$=160$人。
综上,答案依次为:$(1)$$\boldsymbol{45}$,优秀;$(2)$$\boldsymbol{160}$人$\boldsymbol{\surd}$ ;$(3)$ 先算五$(1)$班优秀人数占比$\frac{20}{45}=\frac{4}{9}$,再用五年级总人数$360$乘以该占比$360×\frac{4}{9}=160$人。