1. 用含有字母的式子填空。
(1)一本书a元,12本这样的书(
(2)如下图,涂色部分的面积用字母表示为(
(3)
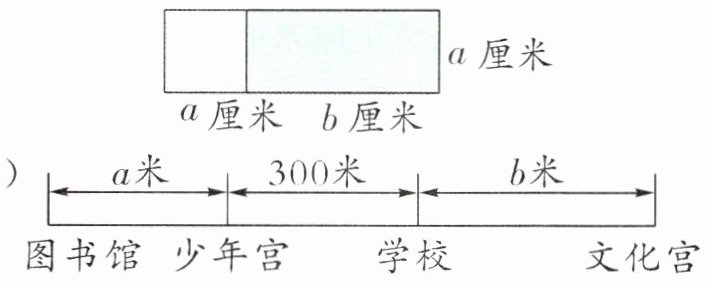
①图书馆到学校的路程是(
②从文化宫到学校比从少年宫到学校远(
③从图书馆到少年宫比从文化宫到少年宫近(
(1)一本书a元,12本这样的书(
12a
)元；50元能买(50÷a
)本这样的书。(2)如下图,涂色部分的面积用字母表示为(
ab
)平方厘米,$a^{2}$平方厘米表示图中(空白
)部分的面积。(3)
①图书馆到学校的路程是(
a+300
)米。②从文化宫到学校比从少年宫到学校远(
b-300
)米。③从图书馆到少年宫比从文化宫到少年宫近(
300+b-a
)米。答案：1.
(1)12a 50÷a 【提示】数量＝总价÷单价
(2)ab 空白 【提示】找出长方形的长和宽，长方形面积＝长×宽。
(3)①a+300 ②b-300 ③300+b-a
【提示】先按题目要求表示出每一段的路程，再相加减。
(1)12a 50÷a 【提示】数量＝总价÷单价
(2)ab 空白 【提示】找出长方形的长和宽，长方形面积＝长×宽。
(3)①a+300 ②b-300 ③300+b-a
【提示】先按题目要求表示出每一段的路程，再相加减。
2. 省略乘号,写出下面各式的结果。
$5× a=$
$c× 1=$
$5× a=$
5a
$t× 0.8=$0.8t
$a× b=$ab
$c× 1=$
c
$11× x=$11x
$b× b=$$b^2$
答案：2.5a 0.8t ab c 11x $b^2$
【提示】数字与字母相乘，数字要写到字母的前面，乘号可以用“·”表示或省略不写，本题要求省略乘号，所以乘号省略不写。
【提示】数字与字母相乘，数字要写到字母的前面，乘号可以用“·”表示或省略不写，本题要求省略乘号，所以乘号省略不写。
3. 跨学科 人体骨骼肌 人体共有600多块骨骼肌,它们附着在骨骼上,形成人体的大体轮廓。满足大致的等量关系：骨骼肌的总质量= 人体体重×0.39。
(1)如果一个人的体重是c千克,那么他的骨骼肌的质量是(
(2)小明的体重是40千克,小明的骨骼肌重(
(1)如果一个人的体重是c千克,那么他的骨骼肌的质量是(
0.39c
)千克。(2)小明的体重是40千克,小明的骨骼肌重(
15.6
)千克。答案：3.
(1)0.39c 【提示】c千克乘0.39，结果简写。
(2)15.6 【提示】当c=40时，0.39×40=15.6。
(1)0.39c 【提示】c千克乘0.39，结果简写。
(2)15.6 【提示】当c=40时，0.39×40=15.6。
4. 找规律在括号里填合适的式子。
(1)1,3,5,…,m,(
(2)2,4,8,16,…,n,(
(1)1,3,5,…,m,(
m+2
),(m+4
)。(2)2,4,8,16,…,n,(
2n
),(4n
)。答案：4.
(1)m+2 m+4 【提示】从第二个数起，后面的数比前一个数大2。
(2)2n 4n 【提示】从第二个数起，后面的数是前一个数的2倍。
(1)m+2 m+4 【提示】从第二个数起，后面的数比前一个数大2。
(2)2n 4n 【提示】从第二个数起，后面的数是前一个数的2倍。
5. 新情境 低碳生活 “低碳生活”是指人们在生活中尽量减少所消耗的能量,从而降低碳(特别是二氧化碳)排放量的一种生活方式。私家车的二氧化碳排放量和耗油量有关,请你根据下表找到二者的关系,并将表格填写完整。
(1)3月份小凯家的私家车耗油a升,这个月他家私家车的二氧化碳排放量是(
(2)在(1)的条件下,当$a= 75$时,这个月他家私家车的二氧化碳排放量是多少千克？
(1)3月份小凯家的私家车耗油a升,这个月他家私家车的二氧化碳排放量是(
2.7a
)千克。(2)在(1)的条件下,当$a= 75$时,这个月他家私家车的二氧化碳排放量是多少千克？
2.7×75=202.5(千克)
答案：13.5 【提示】根据题意可知，私家车每耗油1升，二氧化碳排放量是2.7千克，耗油5升，二氧化碳排放量是2.7×5=13.5(千克)。
(1)2.7a 【提示】耗油a升，二氧化碳排放量是2.7×a=2.7a(千克)。
(2)2.7×75=202.5(千克)
【提示】当a=75时，二氧化碳排放量是2.7a=2.7×75=202.5。
(1)2.7a 【提示】耗油a升，二氧化碳排放量是2.7×a=2.7a(千克)。
(2)2.7×75=202.5(千克)
【提示】当a=75时，二氧化碳排放量是2.7a=2.7×75=202.5。
$10^{2}-$
$(n+1)^{2}-$
$9^2$
$=$19
$(n+1)^{2}-$
$n^2$
$=$$2n+1$
。答案：6.$9^2$ 19 $n^2$ 2n+1 【提示】观察题目可以发现相邻两个自然数的平方数相减，等于这两个自然数相加。
解析：
$9^{2}$ 19 $n^{2}$ $2n+1$
7. 新考法 规律探究 摆
要用6根小棒,摆
要用11根小棒,摆
要用16根小棒……像这样,当摆成6个连在一起的六边形时,需要(
要用6根小棒,摆要用11根小棒,摆要用16根小棒……像这样,当摆成6个连在一起的六边形时,需要(31
)根小棒；如果有721根小棒,那么能摆成(144
)个这样连在一起的六边形；当摆成b个这样连在一起的六边形时,需要(5b+1
)根小棒。答案：7.31 144 5b+1 【提示】摆1个六边形需要6根小棒，可以写成：5×1+1；摆2个连在一起的六边形需要11根小棒，可以写成：5×2+1；摆3个连在一起的六边形需要16根小棒，可以写成：5×3+1；…；由此摆6个连在一起的六边形需要5×6+1=31(根)小棒。可以推理得出摆b个连在一起的六边形需要(5b+1)根小棒；如果有721根小棒，那么能摆成(721-1)÷5=144(个)连在一起的六边形。
解析：
摆1个六边形：$5×1 + 1 = 6$（根）
摆2个六边形：$5×2 + 1 = 11$（根）
摆3个六边形：$5×3 + 1 = 16$（根）
摆6个六边形：$5×6 + 1 = 31$（根）
摆$b$个六边形：$5b + 1$（根）
721根小棒能摆：$(721 - 1)÷5 = 144$（个）
31 144 $5b+1$
摆2个六边形：$5×2 + 1 = 11$（根）
摆3个六边形：$5×3 + 1 = 16$（根）
摆6个六边形：$5×6 + 1 = 31$（根）
摆$b$个六边形：$5b + 1$（根）
721根小棒能摆：$(721 - 1)÷5 = 144$（个）
31 144 $5b+1$