3. 从0~9这10张数字卡片中任意抽取三张,和小数点组成大小不同的两位小数,其中最小的数是多少? 最大的数是多少? 最接近5的小数是什么?
答案:最小的数是0.12,最大的数是9.87,最接近5的小数是5.01
4. 小刚在读一个小数时,把小数点丢了,结果读作三万零六百。已知这个小数读两个零,且这个小数保留整数约等于31。则这个小数是多少?
答案:30.600
解析:
三万零六百写作30600。
因为这个小数保留整数约等于31,所以整数部分是30或31。
若整数部分是31,这个数可能是31.006等,但30600去掉小数点后整数部分为31时,小数部分应为006,即31.006,读作三十一点零零六,读两个零,但31.006保留整数约等于31,符合条件;若整数部分是30,这个数可能是30.600,30.600读作三十点六零零,读两个零,30.600保留整数约等于31,符合条件。
又因为把小数点丢了是30600,30.600去掉小数点是30600,31.006去掉小数点是31006,不符合。所以这个小数是30.600。
30.600
因为这个小数保留整数约等于31,所以整数部分是30或31。
若整数部分是31,这个数可能是31.006等,但30600去掉小数点后整数部分为31时,小数部分应为006,即31.006,读作三十一点零零六,读两个零,但31.006保留整数约等于31,符合条件;若整数部分是30,这个数可能是30.600,30.600读作三十点六零零,读两个零,30.600保留整数约等于31,符合条件。
又因为把小数点丢了是30600,30.600去掉小数点是30600,31.006去掉小数点是31006,不符合。所以这个小数是30.600。
30.600
5. 小明设计了一个程序,输入相应的代码,输出的结果如下图(例如:保留整数,结果就显示6)。已知$□ +◯ +◯ +\triangle =30$,则这个三位小数是多少?
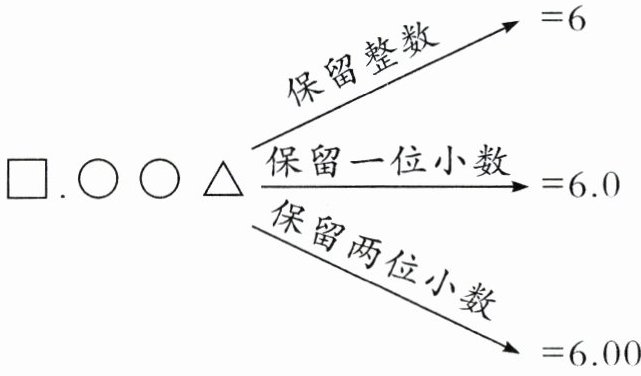

答案:5.997
解析:
设这个三位小数为$□.◯◯\triangle$,其中$□$为整数部分,$◯$为十分位和百分位数字,$\triangle$为千分位数字。
由保留整数结果为$6$,得$□ = 5$(因保留整数看十分位,若$□=6$则保留整数至少为$6$,但结合保留一位小数为$6.0$,整数部分只能为$5$)。
保留一位小数为$6.0$,则$5.95\leqslant5.◯◯\triangle<6.05$,且十分位$◯=9$(否则无法进位到$6.0$)。
保留两位小数为$6.00$,则$5.995\leqslant5.◯◯\triangle<6.005$,故百分位$◯=9$,千分位$\triangle\geqslant5$。
已知$□ + ◯ + ◯ + \triangle=30$,即$5 + 9 + 9 + \triangle=30$,解得$\triangle=7$。
这个三位小数是$5.997$。
$5.997$
由保留整数结果为$6$,得$□ = 5$(因保留整数看十分位,若$□=6$则保留整数至少为$6$,但结合保留一位小数为$6.0$,整数部分只能为$5$)。
保留一位小数为$6.0$,则$5.95\leqslant5.◯◯\triangle<6.05$,且十分位$◯=9$(否则无法进位到$6.0$)。
保留两位小数为$6.00$,则$5.995\leqslant5.◯◯\triangle<6.005$,故百分位$◯=9$,千分位$\triangle\geqslant5$。
已知$□ + ◯ + ◯ + \triangle=30$,即$5 + 9 + 9 + \triangle=30$,解得$\triangle=7$。
这个三位小数是$5.997$。
$5.997$
附加题。(共10分,不计入总分)
一个两位小数,小数部分在计数器上表示需要5个算珠;整数部分是一个两位数,在计数器上表示需要4个算珠。这样的两位小数可能是多少?
一个两位小数,小数部分在计数器上表示需要5个算珠;整数部分是一个两位数,在计数器上表示需要4个算珠。这样的两位小数可能是多少?
答案:13.14、13.41、13.50、13.05、13.23、13.32、22.14、22.41、22.50、22.05、22.23、22.32、31.14、31.41、31.50、31.05、31.23、31.32、40.14、40.41、40.50、40.05、40.23、40.32
解析:
13.05、13.14、13.23、13.32、13.41、13.50、22.05、22.14、22.23、22.32、22.41、22.50、31.05、31.14、31.23、31.32、31.41、31.50、40.05、40.14、40.23、40.32、40.41、40.50