1. 新情境 粮食总产量 粮食总产量关系国计民生,维系国家安全,是反映经济社会发展的重要基础性指标。2024年我国粮食总产量比2023年增长$\frac{2}{125}$,是把
2023 年我国粮食总产量
看作单位“1”,2024年我国的粮食总产量约是2023年产量的$\frac{127}{125}$或$1+\frac{2}{125}$
,数量关系:2023年我国粮食总产量×$\frac{127}{125}$或$1+\frac{2}{125}$
= 2024年我国粮食总产量。答案:2023 年我国粮食总产量
$\frac{127}{125}$或$1+\frac{2}{125}$ $\frac{127}{125}$或$1+\frac{2}{125}$
【提示】在某个量的基础上增加,可以将这个量看作单位“1”。
$\frac{127}{125}$或$1+\frac{2}{125}$ $\frac{127}{125}$或$1+\frac{2}{125}$
【提示】在某个量的基础上增加,可以将这个量看作单位“1”。
2. 看图列式计算。
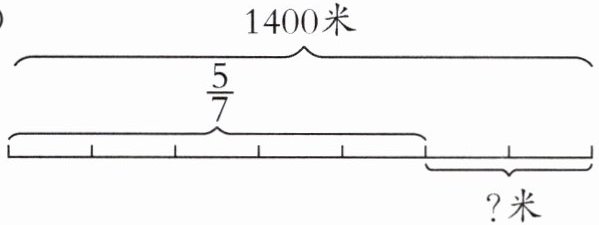
(1)
(2)

(1)

(2)

答案:
(1)$1400×(1-\frac{5}{7})=400$(米)
(2)$264×(1+\frac{3}{4})=462$(人)
【提示】先求出未知量占已知量的分率,再用乘法计算,即可得出答案。
(1)$1400×(1-\frac{5}{7})=400$(米)
(2)$264×(1+\frac{3}{4})=462$(人)
【提示】先求出未知量占已知量的分率,再用乘法计算,即可得出答案。
3. 新考法 补充问题 根据算式,在横线上补充相应的问题。
修一条长1200米的水渠,第一天修了全长的$\frac{1}{4}$,第二天修了全长的$\frac{1}{3}$。
(1)$1200×(\frac{1}{4}+\frac{1}{3})$
(2)$1200×(\frac{1}{3}-\frac{1}{4})$
(3)$1200×(1-\frac{1}{4}-\frac{1}{3})$
修一条长1200米的水渠,第一天修了全长的$\frac{1}{4}$,第二天修了全长的$\frac{1}{3}$。
(1)$1200×(\frac{1}{4}+\frac{1}{3})$
第一天和第二天一共修了多少米
?(2)$1200×(\frac{1}{3}-\frac{1}{4})$
第二天比第一天多修了多少米或第一天比第二天少修了多少米
?(3)$1200×(1-\frac{1}{4}-\frac{1}{3})$
还剩多少米没有修
?答案:
(1)第一天和第二天一共修了多少米
(2)第二天比第一天多修了多少米或第一天比第二天少修了多少米
(3)还剩多少米没有修
【提示】先确定算式的括号里求的是哪部分占的分率,再确定所求的问题。
(1)第一天和第二天一共修了多少米
(2)第二天比第一天多修了多少米或第一天比第二天少修了多少米
(3)还剩多少米没有修
【提示】先确定算式的括号里求的是哪部分占的分率,再确定所求的问题。
4. 一件冲锋衣原价1600元,提价$\frac{1}{8}后又降价\frac{1}{8}$出售,现在这件冲锋衣比原价贵还是便宜?贵或便宜多少元?
答案:$1600×(1+\frac{1}{8})×(1-\frac{1}{8})=1575$(元)
$1600-1575=25$(元)
现在这件冲锋衣比原价便宜,便宜 25 元。
【提示】提价$\frac{1}{8}$是在 1600 元的基础上增加$\frac{1}{8}$,即$[1600×(1+\frac{1}{8})]$元;降价$\frac{1}{8}$是在$[1600×(1+\frac{1}{8})]$元的基础上减少$\frac{1}{8}$,即$[1600×(1+\frac{1}{8})×(1-\frac{1}{8})]$元;最后再与 1600 元比较计算即可得出答案。
$1600-1575=25$(元)
现在这件冲锋衣比原价便宜,便宜 25 元。
【提示】提价$\frac{1}{8}$是在 1600 元的基础上增加$\frac{1}{8}$,即$[1600×(1+\frac{1}{8})]$元;降价$\frac{1}{8}$是在$[1600×(1+\frac{1}{8})]$元的基础上减少$\frac{1}{8}$,即$[1600×(1+\frac{1}{8})×(1-\frac{1}{8})]$元;最后再与 1600 元比较计算即可得出答案。
5. 六(2)班有45人参加书法小组或绘画小组,每人至少参加其中一个兴趣小组,其中$\frac{2}{3}$的学生参加了书法小组,$\frac{5}{9}$的学生参加了绘画小组。既参加书法小组又参加绘画小组的有多少人?
答案:$45×(\frac{2}{3}+\frac{5}{9}-1)=10$(人)
【提示】既参加书法小组又参加绘画小组的人数占全班人数的$\frac{2}{3}+\frac{5}{9}-1=\frac{2}{9}$,即有$45×\frac{2}{9}=10$(人)。
【提示】既参加书法小组又参加绘画小组的人数占全班人数的$\frac{2}{3}+\frac{5}{9}-1=\frac{2}{9}$,即有$45×\frac{2}{9}=10$(人)。
6. 小军和小敏各收集了一些邮票,小军把自己邮票枚数的$\frac{1}{8}$送给小敏后,两人的邮票枚数就同样多。已知小军原来的邮票比小敏多16枚,则小敏原来有多少枚邮票?
答案:$16÷2÷\frac{1}{8}-16=48$(枚)
【提示】小军原来的邮票比小敏多 16 枚,小军送给小敏$16÷2=8$(枚)邮票后两人邮票枚数相等,则送给小敏的这 8 枚邮票所占的分率为$\frac{1}{8}$,由此可算出小军原来的邮票枚数,进而可算出小敏原来的邮票枚数。
【提示】小军原来的邮票比小敏多 16 枚,小军送给小敏$16÷2=8$(枚)邮票后两人邮票枚数相等,则送给小敏的这 8 枚邮票所占的分率为$\frac{1}{8}$,由此可算出小军原来的邮票枚数,进而可算出小敏原来的邮票枚数。