6. 从前面、右面分别观察一个长方体盒子,看到的形状如图。
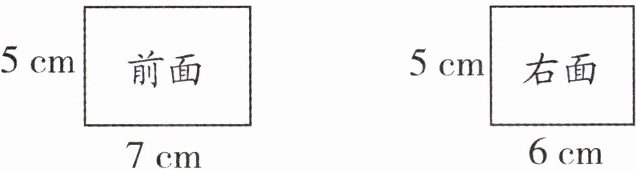
(1)这个长方体的体积是(
(2)如果在它里面放棱长2厘米的正方体,最多可以放(
(3)如果将这个长方体的高增加h厘米,表面积比原来增加(

(1)这个长方体的体积是(
210
)立方厘米。(2)如果在它里面放棱长2厘米的正方体,最多可以放(
18
)个。(3)如果将这个长方体的高增加h厘米,表面积比原来增加(
26h
)平方厘米,体积增加(42h
)立方厘米。(不考虑盒身厚度)答案:
(1)210 提示:由题图可知,该长方体长为7厘米,宽为6厘米,高为5厘米,所以长方体体积V=7×6×5=210(立方厘米)。
(2)18 提示:沿着长最多可以放3个正方体,沿着宽最多可以放3个正方体,沿着高最多可以放2个正方体,一共可以放3×3×2=18(个)正方体。
(3)26h 42h 提示:将这个长方体的高增加h厘米,增加的表面积是长7厘米、宽6厘米、高h厘米的长方体的侧面积,也就是2×6h+2×7h=26h(平方厘米)。增加的体积就是长7厘米、宽6厘米、高h厘米的长方体的体积,也就是7×6h=42h(立方厘米)。
(1)210 提示:由题图可知,该长方体长为7厘米,宽为6厘米,高为5厘米,所以长方体体积V=7×6×5=210(立方厘米)。
(2)18 提示:沿着长最多可以放3个正方体,沿着宽最多可以放3个正方体,沿着高最多可以放2个正方体,一共可以放3×3×2=18(个)正方体。
(3)26h 42h 提示:将这个长方体的高增加h厘米,增加的表面积是长7厘米、宽6厘米、高h厘米的长方体的侧面积,也就是2×6h+2×7h=26h(平方厘米)。增加的体积就是长7厘米、宽6厘米、高h厘米的长方体的体积,也就是7×6h=42h(立方厘米)。
7. 一个长方体玻璃鱼缸,从里面量,长7分米,宽4分米,深5分米。一天,鱼缸的一个面被打碎了,需要把鱼缸转过来盛水,如图。用这个坏的鱼缸,最多能盛水多少升?


答案:7×4×5÷2=70(立方分米) 70立方分米=70升
8. 四名同学观察并测量了一个长方体。
甲:“如果高再增加2分米,它恰好是一个正方体。”
乙:“长方体的前、后、左、右四个面的面积之和是96平方分米。”
丙:“它的底面周长是24分米。”
丁:“这个长方体的棱长总和是64分米。”
四人得到的数据都是正确的,筛选出必要数据作为条件,求出这个长方体的体积。
甲:“如果高再增加2分米,它恰好是一个正方体。”
乙:“长方体的前、后、左、右四个面的面积之和是96平方分米。”
丙:“它的底面周长是24分米。”
丁:“这个长方体的棱长总和是64分米。”
四人得到的数据都是正确的,筛选出必要数据作为条件,求出这个长方体的体积。
答案:答案合理即可,如:选甲、丙所说的数据,则底面边长:24÷4=6(分米) 高:6−2=4(分米) 体积:6×6×4=144(立方分米) 提示:答案不唯一,若选甲、丙所说的数据,则底面边长为24÷4=6(分米),高为6−2=4(分米),因此长方体的体积为6×6×4=144(立方分米)
解析:
选甲、丙所说的数据,底面边长:$24÷4 = 6$(分米),高:$6 - 2=4$(分米),体积:$6×6×4 = 144$(立方分米)。
9. 用一根88厘米长的铁丝围成一个长方体框架,再在外面糊一层纸。已知它的长是高的3倍,宽比长短6厘米。长方体的体积是(
288
)立方厘米。答案:288 提示:根据长方体框架的棱长和是88厘米,可求出长、宽、高的和。假设宽增加6厘米(即长、宽、高的和增加6厘米),则长和宽长度相等,且都是高的3倍,由此可求出长方体的高,从而长方体的长、宽及体积便很容易求出了。本题也可以列方程解答,设高是x厘米,则长是3x厘米,宽是(3x−6)厘米。3x+(3x−6)+x=88÷4,解得x=4,3x=12,3x−6=6,即高是4厘米,长是12厘米,宽是6厘米,体积是12×6×4=288(立方厘米)
解析:
设高是$x$厘米,则长是$3x$厘米,宽是$(3x - 6)$厘米。
$3x + (3x - 6) + x = 88 ÷ 4$
$7x - 6 = 22$
$7x = 28$
$x = 4$
长:$3x = 3 × 4 = 12$(厘米)
宽:$3x - 6 = 12 - 6 = 6$(厘米)
体积:$12 × 6 × 4 = 288$(立方厘米)
288
$3x + (3x - 6) + x = 88 ÷ 4$
$7x - 6 = 22$
$7x = 28$
$x = 4$
长:$3x = 3 × 4 = 12$(厘米)
宽:$3x - 6 = 12 - 6 = 6$(厘米)
体积:$12 × 6 × 4 = 288$(立方厘米)
288
10. 量不变思想 如图,有一个空的长方体容器A和一个盛有水的长方体容器B,水深24厘米。将容器B中的水倒一部分到容器A中,使两个容器中水的高度相等,这时水深是多少厘米?


答案:30×20×24÷(40×30+30×20)=8(厘米) 提示:用长方体容器B内水的体积除以两个容器底面积的和,便可求出两个容器内水的深度。本题也可以列方程解答,设这时水深是x厘米。根据“两个容器里水的体积之和=水的总体积”列方程为40×30×x+30×20×x=30×20×24,1200x+600x=14400,1800x=14400,x=8,即这时水深是8厘米
解析:
设这时水深是$x$厘米。
$40×30× x + 30×20× x=30×20×24$
$1200x + 600x=14400$
$1800x=14400$
$x=8$
答:这时水深是$8$厘米。
$40×30× x + 30×20× x=30×20×24$
$1200x + 600x=14400$
$1800x=14400$
$x=8$
答:这时水深是$8$厘米。
11. 一个长方体的表面积是108平方分米,其中一个面的长是4分米,宽是3分米,这个长方体的体积是多少立方分米?
答案:
108÷2−3×4=42(平方分米) 42÷(4+3)=6(分米) 4×3×6=72(立方分米) 提示:如图,长方体一个顶点处三个相邻面的面积和为108÷2=54(平方分米),其中一个面的面积为3×4=12(平方分米),另两个面展开就是长为(4+3)分米,宽为长方体高的长方形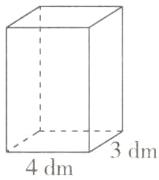
108÷2−3×4=42(平方分米) 42÷(4+3)=6(分米) 4×3×6=72(立方分米) 提示:如图,长方体一个顶点处三个相邻面的面积和为108÷2=54(平方分米),其中一个面的面积为3×4=12(平方分米),另两个面展开就是长为(4+3)分米,宽为长方体高的长方形

12. 有一个长2分米、宽14厘米、高12厘米的长方体,先从这个长方体上切下一个尽可能大的正方体,然后从剩下的部分上再切下一个尽可能大的正方体,最后从第二次剩下的部分上再切下一个尽可能大的正方体。
(1)切了三次后,剩余部分的体积是( )立方厘米。
(2)将切下的三个正方体的表面粘在一起,所得的立体图形的表面积最小是多少平方厘米?
(1)切了三次后,剩余部分的体积是( )立方厘米。
(2)将切下的三个正方体的表面粘在一起,所得的立体图形的表面积最小是多少平方厘米?
答案:
(1)904 提示:从一个长方体上切下一个尽可能大的正方体,要以长方体最短的一条棱的长度为棱长进行切割。2分米=20厘米,如图所示,第一次切下的正方体的棱长是12厘米,20−12=8(厘米),所以第二次切下的正方体的棱长是8厘米,14−8=6(厘米),所以第三次切下的正方体的棱长是6厘米。剩余部分的体积=大长方体的体积−3个正方体的体积=20×14×12−12×12×12−8×8×8−6×6×6=3360−1728−512−216=904(立方厘米)
(2)6×(12×12+8×8+6×6)=1464(平方厘米) 2×(8×8+6×6+4×6)=248(平方厘米) 1464−248=1216(平方厘米) 提示:三个正方体的表面积是固定的,当重合的面最大时,表面积最小。如图,可先求出三个正方体的表面积是6×(12×12+8×8+6×6)=1464(平方厘米),重合的面积=2×(8×8+6×6+4×6)=248(平方厘米),所得立体图形的表面积最小是1464−248=1216(平方厘米)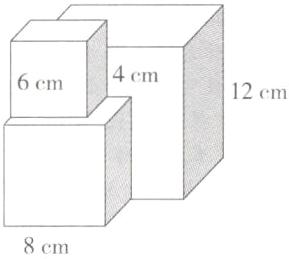
(1)904 提示:从一个长方体上切下一个尽可能大的正方体,要以长方体最短的一条棱的长度为棱长进行切割。2分米=20厘米,如图所示,第一次切下的正方体的棱长是12厘米,20−12=8(厘米),所以第二次切下的正方体的棱长是8厘米,14−8=6(厘米),所以第三次切下的正方体的棱长是6厘米。剩余部分的体积=大长方体的体积−3个正方体的体积=20×14×12−12×12×12−8×8×8−6×6×6=3360−1728−512−216=904(立方厘米)

(2)6×(12×12+8×8+6×6)=1464(平方厘米) 2×(8×8+6×6+4×6)=248(平方厘米) 1464−248=1216(平方厘米) 提示:三个正方体的表面积是固定的,当重合的面最大时,表面积最小。如图,可先求出三个正方体的表面积是6×(12×12+8×8+6×6)=1464(平方厘米),重合的面积=2×(8×8+6×6+4×6)=248(平方厘米),所得立体图形的表面积最小是1464−248=1216(平方厘米)
