8. (2024·江西)如图,从3×4的正方形网格中选择一空白小正方形涂上色,能与涂色部分组成正方体展开图的方法有(
A.1种
B.2种
C.3种
D.4种
B
)A.1种
B.2种
C.3种
D.4种
答案:B
解析:
解:正方体展开图的常见形式有“1-4-1”型、“2-3-1”型、“2-2-2”型、“3-3”型。观察题图中已涂色部分,其形状为“L”型,由4个小正方形组成(假设位置为第2行第2列、第3行第2列、第3行第3列、第4行第3列)。
分析可能的添加位置:
1. 若在第2行第3列添加,可构成“2-3-1”型展开图(第2行2个,第3行2个,第4行1个,调整后符合)。
2. 若在第4行第2列添加,可构成“3-3”型展开图(第3行2个与第4行2个组成3列,符合)。
经检验,其他空白位置添加后均无法形成正方体展开图。能组成正方体展开图的方法有2种。
答案:B
分析可能的添加位置:
1. 若在第2行第3列添加,可构成“2-3-1”型展开图(第2行2个,第3行2个,第4行1个,调整后符合)。
2. 若在第4行第2列添加,可构成“3-3”型展开图(第3行2个与第4行2个组成3列,符合)。
经检验,其他空白位置添加后均无法形成正方体展开图。能组成正方体展开图的方法有2种。
答案:B
9. 如图,去掉这七个正方形中的一个,剩下的平面图形就能成为一个正方体的展开图,则去掉的是标有数字
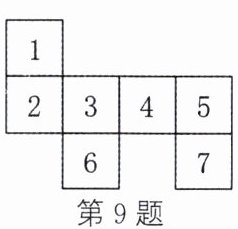
6
或7
的正方形.
答案:6 7
解析:
解:根据正方体展开图的特征,“1-4-1”型展开图中,中间四个正方形为侧面,上下各一个为底面。图中2、3、4、5为中间四个相连的正方形,1、6、7分别在上下及右侧。若保留1、2、3、4、5、6,则符合“1-4-1”型(1在上,6在下);若保留1、2、3、4、5、7,则也符合“1-4-1”型(1在上,7在下)。因此去掉的是标有数字6或7的正方形。
6;7
6;7
10. 如图所示为一个正方体的展开图,则原正方体相对两个面上的数字之和的最小值是
6
.答案:6
解析:
解:将展开图还原成正方体,相对面为:1与5,2与6,3与4。
相对面数字之和分别为:1+5=6,2+6=8,3+4=7。
最小值为6。
答案:6
相对面数字之和分别为:1+5=6,2+6=8,3+4=7。
最小值为6。
答案:6
11. 分别画出从前面、左面和上面观察如图所示的立体图形得到的平面图形.


答案:
如图所示

如图所示

12. 一个几何体是由一些大小相同的小正方体组成的,从前面与左面看得到的平面图形如图所示,则组成这个几何体的小正方体最少有几个?


答案:组成这个几何体的小正方体最少有5个
解析:
解:从前面看,几何体有2列,左列2层,右列1层;从左面看,几何体有2行,前行2层,后行2层。
要使小正方体最少,左列底层2行各1个(共2个),左列上层至少1个(可放在任意一行);右列底层至少1个(需与左列不同行以满足左面看2行2层),右列上层无需小正方体。
最少数量:2(左列底层)+1(左列上层)+1(右列底层)=4?不对,重新分析。
从前面看列数:左2右1;从左面看行数:前2后2。底层需覆盖2行2列,最少4个(2×2)。左列上层至少1个(满足前面看左列2层)。
最少数量:4(底层)+1(左列上层)=5个。
组成这个几何体的小正方体最少有5个。
要使小正方体最少,左列底层2行各1个(共2个),左列上层至少1个(可放在任意一行);右列底层至少1个(需与左列不同行以满足左面看2行2层),右列上层无需小正方体。
最少数量:2(左列底层)+1(左列上层)+1(右列底层)=4?不对,重新分析。
从前面看列数:左2右1;从左面看行数:前2后2。底层需覆盖2行2列,最少4个(2×2)。左列上层至少1个(满足前面看左列2层)。
最少数量:4(底层)+1(左列上层)=5个。
组成这个几何体的小正方体最少有5个。
13. 如图所示为由若干个完全相同的正方体组成的立体图形从上面看所得到的平面图形,正方形上标注的数字表示该位置上正方体的个数.请画出这个立体图形从左面看所得到的平面图形.


答案:
如图所示

如图所示
