7. 下列直线、射线、线段中,能相交的是(

A
)
答案:A
8. 如图,有下列语句:① 直线 $ l $ 经过点 $ A $ 和点 $ B $;② 点 $ A $ 和点 $ B $ 都在直线 $ l $ 上;③ 直线 $ l $ 是 $ A,B $ 两点所确定的直线;④ 线段 $ AB $ 是直线 $ l $ 的一部分. 其中,能正确表达出图形特点的有(
A.$ 1 $ 个
B.$ 2 $ 个
C.$ 3 $ 个
D.$ 4 $ 个
D
)A.$ 1 $ 个
B.$ 2 $ 个
C.$ 3 $ 个
D.$ 4 $ 个
答案:D
解析:
由图可知:
① 直线 $ l $ 经过点 $ A $ 和点 $ B $,正确;
② 点 $ A $ 和点 $ B $ 都在直线 $ l $ 上,正确;
③ 直线 $ l $ 是 $ A,B $ 两点所确定的直线,正确;
④ 线段 $ AB $ 是直线 $ l $ 的一部分,正确。
能正确表达图形特点的有 4 个。
答案:D
① 直线 $ l $ 经过点 $ A $ 和点 $ B $,正确;
② 点 $ A $ 和点 $ B $ 都在直线 $ l $ 上,正确;
③ 直线 $ l $ 是 $ A,B $ 两点所确定的直线,正确;
④ 线段 $ AB $ 是直线 $ l $ 的一部分,正确。
能正确表达图形特点的有 4 个。
答案:D
9. 根据下列要求画图:① 延长直线 $ AB $ 至点 $ C $;② 延长射线 $ AB $ 至点 $ C $;③ 反向延长射线 $ AB $ 至点 $ C $;④ 延长线段 $ AB $ 至点 $ C $;⑤ 反向延长线段 $ AB $ 至点 $ C $. 其中,正确的要求有(
A.$ 1 $ 个
B.$ 2 $ 个
C.$ 3 $ 个
D.$ 4 $ 个
C
)A.$ 1 $ 个
B.$ 2 $ 个
C.$ 3 $ 个
D.$ 4 $ 个
答案:C
解析:
解:①直线AB本身是无限延伸的,不能延长,故①错误;
②射线AB端点为A,向B方向无限延伸,不能延长射线AB至点C,故②错误;
③反向延长射线AB至点C,即将射线AB从端点A向相反方向延长,正确;
④延长线段AB至点C,正确;
⑤反向延长线段AB至点C,正确。
综上,正确的要求有③④⑤,共3个。
答案:C
②射线AB端点为A,向B方向无限延伸,不能延长射线AB至点C,故②错误;
③反向延长射线AB至点C,即将射线AB从端点A向相反方向延长,正确;
④延长线段AB至点C,正确;
⑤反向延长线段AB至点C,正确。
综上,正确的要求有③④⑤,共3个。
答案:C
10. 值日生小明想把教室桌椅摆放整齐,为了将一列课桌对齐,他把这列课桌的最前面一张和最后面一张先拉成一条线,其余课桌按这条直线摆放,这样做用到的数学知识为
两点确定一条直线
.答案:两点确定一条直线
11. (易错题)平面上有 $ A,B,C $ 三点,经过其中任意两点画一条直线,可以画出直线
1或3
条.答案:1或3 [易错分析]考虑不周全导致漏解.
解析:
解:分两种情况:
①当A、B、C三点在同一条直线上时,只能画1条直线;
②当A、B、C三点不在同一条直线上时,能画3条直线。
故可以画出直线1或3条。
1或3
①当A、B、C三点在同一条直线上时,只能画1条直线;
②当A、B、C三点不在同一条直线上时,能画3条直线。
故可以画出直线1或3条。
1或3
12. (易错题)如果 $ A $ 市与 $ B $ 市之间是直达快车,那么铁道部门要为这次列车准备
2
种不同的车票. 如果是某普通列车,且途中要经过 $ 4 $ 个停靠站点(不包括起始站和终点站),那么铁道部门要为这次列车准备15
种不同票价(相同路段票价相同)的车票,30
种不同的车票.答案:2 15 30 [易错分析]忽视车票具有方向性致错.
解析:
12. 2;15;30
解:
直达快车:A市与B市为2个站点,车票有A→B和B→A,共2种。
普通列车:途中经4个停靠站,总站点数为2+4=6个。不同票价的车票种数为从6个站点中任选2个的组合数,即$C_{6}^{2}=\frac{6×5}{2×1}=15$种;不同车票种数为从6个站点中任选2个的排列数,即$A_{6}^{2}=6×5=30$种。
解:
直达快车:A市与B市为2个站点,车票有A→B和B→A,共2种。
普通列车:途中经4个停靠站,总站点数为2+4=6个。不同票价的车票种数为从6个站点中任选2个的组合数,即$C_{6}^{2}=\frac{6×5}{2×1}=15$种;不同车票种数为从6个站点中任选2个的排列数,即$A_{6}^{2}=6×5=30$种。
13. 如图,按照下列语句画出图形:
(1)连接 $ AC,BD $,使它们相交于点 $ F $;
(2)延长线段 $ BA,DE $,使它们相交于点 $ G $;
(3)反向延长线段 $ EA,DC $,使它们相交于点 $ H $;
(4)画射线 $ EC $;
(5)取一点 $ P $,使点 $ P $ 既在直线 $ AB $ 上又在直线 $ CD $ 上.

(1)连接 $ AC,BD $,使它们相交于点 $ F $;
(2)延长线段 $ BA,DE $,使它们相交于点 $ G $;
(3)反向延长线段 $ EA,DC $,使它们相交于点 $ H $;
(4)画射线 $ EC $;
(5)取一点 $ P $,使点 $ P $ 既在直线 $ AB $ 上又在直线 $ CD $ 上.

答案:
如图所示
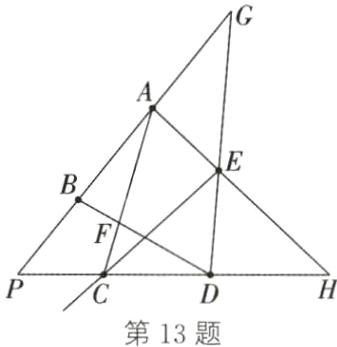
如图所示

14. 如图,在一条直线上取两个点 $ A,B $,共得多少条线段?在一条直线上取三个点 $ A,B,C $,共得多少条线段?在一条直线上取四个点 $ A,B,C,D $,共得多少条线段?在一条直线上取 $ n $($ n $ 为大于 $ 1 $ 的正整数)个点,共得多少条线段?


答案:在一条直线上取两个点A,B,共得1条线段 取三个点A,B,C,共得2 + 1 = 3(条)线段 取四个点A,B,C,D,共得3 + 2 + 1 = 6(条)线段 取n(n为大于1的正整数)个点,共得(n - 1) + (n - 2) + … + 3 + 2 + 1 = $\frac{n(n - 1)}{2}$(条)线段