+跟踪练习3 ____里最大能填几?
49
652>6
____
49
5
<496 652>6
4
8 ____
9
89>760>__7
58答案:5 4 9 7
解析:
1. 49__<496
解:百位和十位相同,个位需小于6,最大填5。
2. 652>6__8
解:百位相同,十位需小于5(因个位2<8),最大填4。
3. __89>760>__58
解:
左空:十位8>6,百位最小填7,最大填9;
右空:760>__58,百位最大填7(758<760)。
答案:5;4;9;7
解:百位和十位相同,个位需小于6,最大填5。
2. 652>6__8
解:百位相同,十位需小于5(因个位2<8),最大填4。
3. __89>760>__58
解:
左空:十位8>6,百位最小填7,最大填9;
右空:760>__58,百位最大填7(758<760)。
答案:5;4;9;7
例3菲菲家的门牌号码是一个
三位数,个位上的数字比十位上
的数字大3,百位上的数字比个
位上的数字小5。菲菲家的门牌
号码可能是多少?
三位数,个位上的数字比十位上
的数字大3,百位上的数字比个
位上的数字小5。菲菲家的门牌
号码可能是多少?
答案:
思路分析根据题中给出的条件,可以先推出个位上的数字。
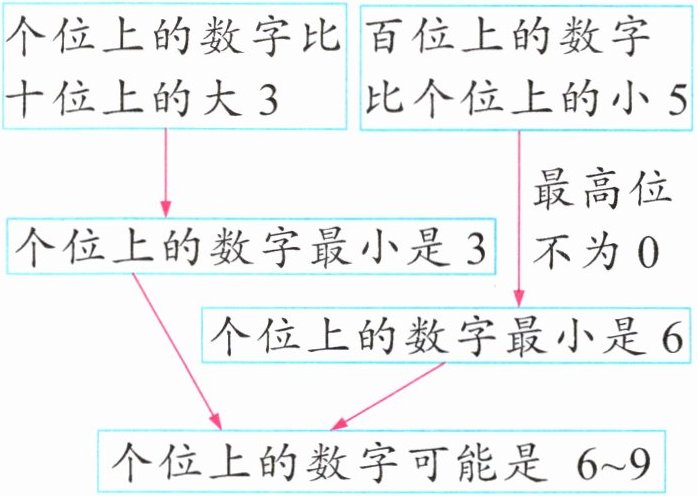
由个位上的数字分别列举:

+规范解答菲菲家的门牌号可能是136或247或358或469。
思路分析根据题中给出的条件,可以先推出个位上的数字。

由个位上的数字分别列举:

+规范解答菲菲家的门牌号可能是136或247或358或469。
跟踪练习4 一个三位数,百位上的数字比个位上的数字大2,各个数位上的数字之和是8,读这个数时要读一个“零”。这个三位数是(
503
)。答案:503
解析:
设这个三位数个位数字为$x$,则百位数字为$x + 2$,十位数字为$y$。
由题意得:
1. $x + (x + 2) + y = 8$,化简得$2x + y = 6$;
2. 读这个数时要读一个“零”,所以十位数字$y = 0$(且个位数字$x \neq 0$)。
当$y = 0$时,$2x = 6$,解得$x = 3$。
百位数字为$x + 2 = 3 + 2 = 5$。
所以这个三位数是$503$。
答案:$503$
由题意得:
1. $x + (x + 2) + y = 8$,化简得$2x + y = 6$;
2. 读这个数时要读一个“零”,所以十位数字$y = 0$(且个位数字$x \neq 0$)。
当$y = 0$时,$2x = 6$,解得$x = 3$。
百位数字为$x + 2 = 3 + 2 = 5$。
所以这个三位数是$503$。
答案:$503$