例1(教材P78)从下图中找出两个数,使它们的和等于56,可以怎样找?你能从中找出两个数,使它们的和等于65吗?
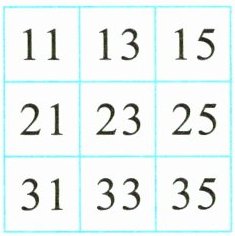

答案:思路分析 先观察图中的数,都是大于2的单数,且每行相邻的两个数相差2。前一问中,要看找出的两个数的个位上的数字相加的和是不是等于6,十位上的数字相加的和是不是等于50,由此找到 $21 + 35 = 56$,$31 + 25 = 56$,$23 + 33 = 56$。后一问中,因为单数加单数,结果一定是双数,65是单数,所以从表中找不出两个数的和等于65。
规范解答 可以找出 $21 + 35$,$31 + 25$,$23 + 33$ 的和等于56;不能从中找出两个数,使它们的和等于65。
规范解答 可以找出 $21 + 35$,$31 + 25$,$23 + 33$ 的和等于56;不能从中找出两个数,使它们的和等于65。
跟踪练习1 从下表里找出两个数,使它们的和等于34,可以怎样找?你能从中找出两个数,使它们的和等于37吗?


答案:可以找出 $2 + 32$,$6 + 28$,$8 + 26$,$12 + 22$,$16 + 18$ 的和等于 $34$;不能从中找出两个数,使它们的和等于 $37$。
解析:
解:和等于34的两个数:2+32,6+28,8+26,12+22,16+18;
不能找出两个数的和等于37。
不能找出两个数的和等于37。
例2(教材P85)在“数塔”空格里填合适的数。


90 52 29 36 17 14 12
答案:思路分析 先比较最底层和倒数第二层的数,再比较倒数第二层和倒数第三层的数,可以发现规律:下面相邻两个数的和就是这两个数上面的一个数。由此推算出第一题空格里的数自下而上分别是 $15 + 14 = 29$,$23 + 29 = 52$,$38 + 52 = 90$。第二题空格里的数自上而下分别是 $83 - 47 = 36$,$36 - 19 = 17$,$28 - 14 = 14$,$17 - 5 = 12$。
规范解答 90 52 29 36 17 14 12
规范解答 90 52 29 36 17 14 12