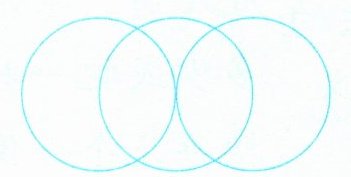
例1 (教材P27)在下图中画8个$\triangle$,使每个圆里都有4个$\triangle$。
思路分析 每个圆里都有4个$\triangle$,有3个圆,一共要画$4×3 = 12$(个)$\triangle$。但题中要求只能画8个$\triangle$,所以有$12 - 8 = 4$(个)$\triangle$是合用的。仔细观察3个圆,发现第二个圆分别与第一个、第三个圆相交,共有2个重叠部分,只要这2个重叠部分$\triangle$的个数和是4即可,然后根据重叠部分$\triangle$的个数,确定非重叠部分$\triangle$的个数。
规范解答 画法不唯一,如：
思路分析 每个圆里都有4个$\triangle$,有3个圆,一共要画$4×3 = 12$(个)$\triangle$。但题中要求只能画8个$\triangle$,所以有$12 - 8 = 4$(个)$\triangle$是合用的。仔细观察3个圆,发现第二个圆分别与第一个、第三个圆相交,共有2个重叠部分,只要这2个重叠部分$\triangle$的个数和是4即可,然后根据重叠部分$\triangle$的个数,确定非重叠部分$\triangle$的个数。
规范解答 画法不唯一,如：
答案：解析：本题主要考查对图形数量分配以及重叠部分数量关系的理解和运用，通过分析每个圆所需图形数量、总数量要求以及圆与圆之间的相交关系来确定图形的具体画法。
答案：图略（按照分析，在三个相交圆的重叠部分合理分配$\triangle$，使每个圆里都有4个$\triangle$即可，有多种画法）。
答案：图略（按照分析，在三个相交圆的重叠部分合理分配$\triangle$，使每个圆里都有4个$\triangle$即可，有多种画法）。
跟踪练习1 新素养 推理意识 请在图中画13个$◯$,使每个大四边形里都有4个$◯$。
答案：
画法不唯一，如：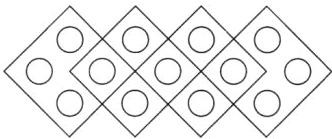
画法不唯一，如：
例2 (教材P32)有一堆糖,比20粒多,比40粒少。平均分给一些小朋友,每人分得的粒数和小朋友的人数同样多。可能有多少粒糖？有多少个小朋友？
思路分析 每人分得的粒数和小朋友的人数同样多,且糖的总粒数在20至40之间,因此只要想哪两个相同的数相乘的积在此范围内,想对应的乘法口诀即可,符合条件的乘法口诀有两句,即“五五二十五”和“六六三十六”。
规范解答 可能有25粒糖,有5个小朋友；也可能有36粒糖,有6个小朋友。
思路分析 每人分得的粒数和小朋友的人数同样多,且糖的总粒数在20至40之间,因此只要想哪两个相同的数相乘的积在此范围内,想对应的乘法口诀即可,符合条件的乘法口诀有两句,即“五五二十五”和“六六三十六”。
规范解答 可能有25粒糖,有5个小朋友；也可能有36粒糖,有6个小朋友。
答案：解析：
本题考查的是利用乘法口诀解决实际问题。
由于糖的总数在20至40之间，每人分得的粒数和小朋友的人数同样多。
因此，需要找到两个相同的数相乘，其积在20至40之间。
符合条件的乘法口诀是“五五二十五”和“六六三十六”。
根据乘法口诀“五五二十五”，可得：
$5 × 5 = 25$
即可能有25粒糖，5个小朋友，每人分得5粒糖。
根据乘法口诀“六六三十六”，可得：
$6 × 6 = 36$
即可能有36粒糖，6个小朋友，每人分得6粒糖。
答案：
可能有25粒糖，有5个小朋友；也可能有36粒糖，有6个小朋友。
本题考查的是利用乘法口诀解决实际问题。
由于糖的总数在20至40之间，每人分得的粒数和小朋友的人数同样多。
因此，需要找到两个相同的数相乘，其积在20至40之间。
符合条件的乘法口诀是“五五二十五”和“六六三十六”。
根据乘法口诀“五五二十五”，可得：
$5 × 5 = 25$
即可能有25粒糖，5个小朋友，每人分得5粒糖。
根据乘法口诀“六六三十六”，可得：
$6 × 6 = 36$
即可能有36粒糖，6个小朋友，每人分得6粒糖。
答案：
可能有25粒糖，有5个小朋友；也可能有36粒糖，有6个小朋友。