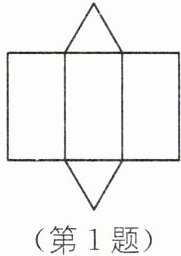
1. 教材 P149 习题 T1·变式(2024·扬州中考)如图是某几何体的表面展开后得到的平面图形,则该几何体是(
C
). A. 三棱锥 B. 圆锥 C. 三棱柱 D. 长方体 答案：C
解析：
该几何体的表面展开图由两个三角形和三个长方形组成，两个三角形为底面，三个长方形为侧面，符合三棱柱的展开图特征。
C
C
2.(2025·广西玉林玉州区期末)如图所示是一个小正方体的展开图,把展开图折叠成小正方体后,有“和”字一面的相对面的字是(
B
). A. 和 B. 社 C. 谐 D. 会 答案：B
解析：
将展开图折叠成小正方体，“和”字与“社”字所在的面不相邻，为相对面。
B
B
3.(2024·常州中考)下列图形中,为四棱锥的侧面展开图的是(
B
). A. B. C. D. 答案：B
4. 如图是一个正方体纸盒的展开图,如果这个正方体纸盒相对两个面上的代数式的值相等,那么代数式 $3a - 2b + c$ 的值为
11
. 答案：11 [解析]由正方体表面展开图，得标注“8 - c”与“3c - 4”的面是相对的面，标注“a + 3”与“5”的面是相对的面，标注“b - 1”与“4b + 2”的面是相对的面。因为相对两个面上的代数式的值相等，所以8 - c = 3c - 4，a + 3 = 5，b - 1 = 4b + 2，解得a = 2，b = - 1，c = 3，所以3a - 2b + c = 6 + 2 + 3 = 11。
思路引导 本题考查了正方体相对两个面上的文字。根据正方体的平面展开图的特点，相对的两个面中间一定隔着一个小正方形，且没有公共边和公共顶点，即“对面无邻点”，依此来找相对面。
思路引导 本题考查了正方体相对两个面上的文字。根据正方体的平面展开图的特点，相对的两个面中间一定隔着一个小正方形，且没有公共边和公共顶点，即“对面无邻点”，依此来找相对面。
5. 有一个正方体,在它的各个面上分别标上数字1,2,3,4,5,6,甲、乙、丙三位同学从三个不同的角度去观察此正方体,观察结果如图所示： 
请画出正方体的一种表面展开图.(要求把数字标注在表面展开图中)
请画出正方体的一种表面展开图.(要求把数字标注在表面展开图中)答案：
从3个小立方体上的数可知，与写有数字1的面相邻的面上数字是2，3，4，6，所以数字1面对数字5面，同理，正方体面上数字3对6，故正方体面上数字2对4。故作出的平面展开图如图所示。(答案不唯一)
从3个小立方体上的数可知，与写有数字1的面相邻的面上数字是2，3，4，6，所以数字1面对数字5面，同理，正方体面上数字3对6，故正方体面上数字2对4。故作出的平面展开图如图所示。(答案不唯一)
6.(2024·宜宾中考)如图是正方体表面展开图.将其折叠成正方体后,距顶点A最远的点是(
A
). A. B点 B. C点 C. D点 D. E点 答案：A [解析]由图可知，A对应 - 1，B对应2，C对应0。因为 - 1的相反数为1，2的相反数为 - 2，0的相反数为0，所以A = 1，B = - 2，C = 0。故选A。
7.(湖南株洲二中自主招生)如图所示是一个正方体盒的平面展开图,如果在其中的三个正方形A,B,C中分别填入适当的数,使得它们折成正方体后,相对的面上的两个数互为相反数,那么填入A,B,C的三个数依次是(
A
). A. 1,-2,0 B. -1,2,0 C. -2,0,1 D. -2,1,0 答案：A [解析]由题意，得3和4是相对面，2和5是相对面，1和6是相对面，
∴滚动1次后，骰子朝下一面的数字是2，滚动2次后，骰子朝下一面的数字是3，滚动3次后，骰子朝下一面的数字是5，滚动4次后，骰子朝下一面的数字是4，滚动5次后，骰子朝下一面的数字是2，…，
∴2025÷4 = 506……1，每4次循环一次，
∴滚动2025次后，骰子朝下一面的数字是2。故选A。
∴滚动1次后，骰子朝下一面的数字是2，滚动2次后，骰子朝下一面的数字是3，滚动3次后，骰子朝下一面的数字是5，滚动4次后，骰子朝下一面的数字是4，滚动5次后，骰子朝下一面的数字是2，…，
∴2025÷4 = 506……1，每4次循环一次，
∴滚动2025次后，骰子朝下一面的数字是2。故选A。
8. 类推思想(2025·安徽合肥包河区期末)有一个正六面体的骰子放在桌面上,将骰子按如图所示顺时针方向滚动,每滚动90°算一次,则滚动2025次后,骰子朝下一面的数字是(
B
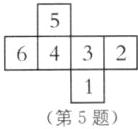
). A. 2 B. 3 C. 4 D. 5 答案：12 [解析]由题意可知，“3点”的面的邻面有“2点、6点、4点、5点”，所以与“3点”相对的面的点数为“1点”；因为“4点”的面的邻面有“6点、5点、3点、1点”，所以与“4点”相对的面的点数为“2点”；所以与“6点”相对的面的点数为“5点”，所以长方体底面上的点数之和是4 + 1 + 5 + 2 = 12。