8. 如图,A,B,C,D,E五个城市,它们之间原有道路相通,现在打算在C,E两城市之间沿直线再修建一条公路,这条公路与原公路的交叉处必须设立交桥,问怎样确定立交桥的位置?应架设几座立交桥?
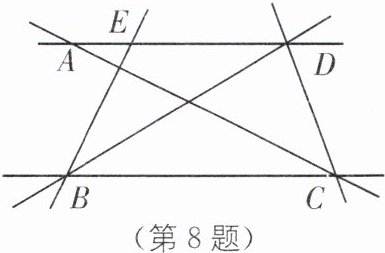

答案:连接CE,CE与BD的交点处就是架设立交桥的位置,应架设1座立交桥.
9. 中考新考法 规律探究 (1)观察图(1),由点A和点B可确定______条直线.
观察图(2),由不在同一直线上的三点A,B和C最多能确定______条直线.
(2)动手画一画图(3)中经过A,B,C,D四点中任意两点的所有直线,最多共可作______条直线.
(3)在同一平面内不在同一直线上的五个点最多能确定几条直线?并求出n个点(n≥2)最多能确定几条直线.

观察图(2),由不在同一直线上的三点A,B和C最多能确定______条直线.
(2)动手画一画图(3)中经过A,B,C,D四点中任意两点的所有直线,最多共可作______条直线.
(3)在同一平面内不在同一直线上的五个点最多能确定几条直线?并求出n个点(n≥2)最多能确定几条直线.

答案:
(1)1 3
(2)6(图略)
(3)如图,有不在同一直线上的五个点A,B,C,D,E,

连接其中任意两点,最多能确定10条直线.当有n个点时,每个点都可以确定(n−1)条直线,但每条直线都重复算了1遍,如:直线AC与直线CA是同一条直线,故n个点最多能确定$\frac{n(n−1)}{2}$条直线.
素养考向 本题是一道规律探究题,考查了由点确定直线的相关知识,有一定的难度,注意动手操作及总结规律能力的培养.
(1)1 3
(2)6(图略)
(3)如图,有不在同一直线上的五个点A,B,C,D,E,

连接其中任意两点,最多能确定10条直线.当有n个点时,每个点都可以确定(n−1)条直线,但每条直线都重复算了1遍,如:直线AC与直线CA是同一条直线,故n个点最多能确定$\frac{n(n−1)}{2}$条直线.
素养考向 本题是一道规律探究题,考查了由点确定直线的相关知识,有一定的难度,注意动手操作及总结规律能力的培养.
10. 数学抽象思维 (1)[观察思考]如图,线段AB上有两个点C,D,请分别写出以点A,B,C,D为端点的线段,并计算图中共有多少条线段.
(2)[模型构建]如果线段上有m个点(包括线段的两个端点),则该线段上共有多少条线段?请说明你结论的正确性.
(3)[拓展应用]某班45名同学在毕业后的一次聚会中,若每两人握1次手问好,那么共握多少次手?(请将这个问题转化为上述模型,并直接应用上述模型的结论解决问题)

(2)[模型构建]如果线段上有m个点(包括线段的两个端点),则该线段上共有多少条线段?请说明你结论的正确性.
(3)[拓展应用]某班45名同学在毕业后的一次聚会中,若每两人握1次手问好,那么共握多少次手?(请将这个问题转化为上述模型,并直接应用上述模型的结论解决问题)

答案:
(1)以点A为左端点的线段有线段AC,AD,AB,以点C为左端点的线段有线段CD,CB,以点D为左端点的线段有线段DB,
∴共有3+2+1=6(条)线段.
(2)设该线段上共有线段x条,则$x=(m-1)+(m-2)+\cdots +3+2+1$,①
∴$x=1+2+3+\cdots +(m-2)+(m-1)$,②①+②,得$2x=m+m+\cdots +m=m(m-1)$.
∴$x=\frac{1}{2}m(m-1)$.故该线段上共有$\frac{1}{2}m(m-1)$条线段.
(3)把45名同学看作线段上的45个点,每两名同学之间的1次握手看作1条线段,线段上有45个点,则该线段上共有线段的条数就等于握手的次数,因此一共要握手$\frac{1}{2}× 45× (45-1)=990$(次).
(1)以点A为左端点的线段有线段AC,AD,AB,以点C为左端点的线段有线段CD,CB,以点D为左端点的线段有线段DB,
∴共有3+2+1=6(条)线段.
(2)设该线段上共有线段x条,则$x=(m-1)+(m-2)+\cdots +3+2+1$,①
∴$x=1+2+3+\cdots +(m-2)+(m-1)$,②①+②,得$2x=m+m+\cdots +m=m(m-1)$.
∴$x=\frac{1}{2}m(m-1)$.故该线段上共有$\frac{1}{2}m(m-1)$条线段.
(3)把45名同学看作线段上的45个点,每两名同学之间的1次握手看作1条线段,线段上有45个点,则该线段上共有线段的条数就等于握手的次数,因此一共要握手$\frac{1}{2}× 45× (45-1)=990$(次).
11. (2024·吉林中考)如图,从长春站去往胜利公园,与其他道路相比,走人民大街路程最近,其蕴含的数学道理是
两点之间,线段最短
.答案:两点之间,线段最短