9. 如图,直线AB,CD相交于点O,OE⊥CD,且∠BOD的度数是∠AOD的5倍. 求:
(1)∠AOD,∠BOD的度数;
(2)∠BOE的度数.

(1)∠AOD,∠BOD的度数;
(2)∠BOE的度数.

答案:
(1)
∵AB是直线,
∴∠BOD+∠AOD=180°.
∵∠BOD的度数是∠AOD的5倍,
∴∠AOD=$\frac{1}{6}$×180°=30°,∠BOD=$\frac{5}{6}$×180°=150°.
(2)
∵OE⊥DC,
∴∠DOE=90°.
∴∠BOE=∠BOD−∠DOE=150°−90°=60°.
(1)
∵AB是直线,
∴∠BOD+∠AOD=180°.
∵∠BOD的度数是∠AOD的5倍,
∴∠AOD=$\frac{1}{6}$×180°=30°,∠BOD=$\frac{5}{6}$×180°=150°.
(2)
∵OE⊥DC,
∴∠DOE=90°.
∴∠BOE=∠BOD−∠DOE=150°−90°=60°.
10. 如图,直线AB,CD相交于点O,OE平分∠BOC,OF⊥CD. 若∠BOD∶∠BOE= 1∶4,求∠AOF的度数.


答案:设∠BOD=x°,则∠BOE=4x°.
∵OE平分∠BOC,
∴∠BOC=2∠BOE=8x°.
∵∠BOD+∠BOC=180°,
∴x+8x=180,
∴x=20,
∴∠AOC=∠BOD=x°=20°.
∵OF⊥CD,
∴∠COF=90°,
∴∠AOF=90°−∠AOC=70°.
∵OE平分∠BOC,
∴∠BOC=2∠BOE=8x°.
∵∠BOD+∠BOC=180°,
∴x+8x=180,
∴x=20,
∴∠AOC=∠BOD=x°=20°.
∵OF⊥CD,
∴∠COF=90°,
∴∠AOF=90°−∠AOC=70°.
11. 分类讨论思想 (2024·无锡惠山区期末)已知点O为直线AB上一点,过点O作射线OC,∠BOC= 110°.

(1)如图(1),则∠AOC的度数为______°;
(2)如图(2),过点O在直线AB下方作射线OD,使OD⊥OC,作∠AOC的平分线OM,求∠MOD的度数;
(3)在(2)的条件下,作射线OP,若∠BOP与∠AOM互余,求∠COP的度数.

(1)如图(1),则∠AOC的度数为______°;
(2)如图(2),过点O在直线AB下方作射线OD,使OD⊥OC,作∠AOC的平分线OM,求∠MOD的度数;
(3)在(2)的条件下,作射线OP,若∠BOP与∠AOM互余,求∠COP的度数.
答案:
(1)70 [解析]
∵∠BOC=110°,
∴∠AOC=180°−∠BOC=70°.
(2)由
(1)可知,∠AOC=70°,
∵OD⊥OC,
∴∠COD=90°.
∵OM为∠AOC的平分线,
∴∠COM=∠AOM=$\frac{1}{2}$∠AOC=$\frac{1}{2}$×70°=35°,
∴∠MOD=∠COD−∠COM=90°−35°=55°.
(3)由
(2)可知,∠AOM=35°.
∵∠BOP与∠AOM互余,
∴∠BOP+∠AOM=90°,∠BOP=90°−∠AOM=90°−35°=55°.
当射线OP在∠BOC内部时,如图
(1),
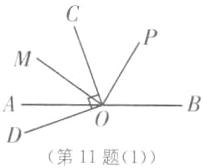
∠COP=∠BOC−∠BOP=110°−55°=55°;
当射线OP在∠BOC外部时,如图
(2),

∠COP=∠BOC+∠BOP=110°+55°=165°.
综上所述,∠COP的度数为55°或165°.
(1)70 [解析]
∵∠BOC=110°,
∴∠AOC=180°−∠BOC=70°.
(2)由
(1)可知,∠AOC=70°,
∵OD⊥OC,
∴∠COD=90°.
∵OM为∠AOC的平分线,
∴∠COM=∠AOM=$\frac{1}{2}$∠AOC=$\frac{1}{2}$×70°=35°,
∴∠MOD=∠COD−∠COM=90°−35°=55°.
(3)由
(2)可知,∠AOM=35°.
∵∠BOP与∠AOM互余,
∴∠BOP+∠AOM=90°,∠BOP=90°−∠AOM=90°−35°=55°.
当射线OP在∠BOC内部时,如图
(1),

∠COP=∠BOC−∠BOP=110°−55°=55°;
当射线OP在∠BOC外部时,如图
(2),

∠COP=∠BOC+∠BOP=110°+55°=165°.
综上所述,∠COP的度数为55°或165°.
12. (2024·雅安中考)如图,直线AB,CD交于点O,OE⊥AB于O,若∠1= 35°,则∠2的度数是(

A.55°
B.45°
C.35°
D.30°
A
).
A.55°
B.45°
C.35°
D.30°
答案:A
解析:
∵OE⊥AB,
∴∠AOE=90°,
∵∠1=35°,
∴∠AOC=∠AOE - ∠1=90° - 35°=55°,
∵∠2与∠AOC是对顶角,
∴∠2=∠AOC=55°。
A