1. (2025·扬州期末)如图,下列条件不能判定$AB // CD$的是(
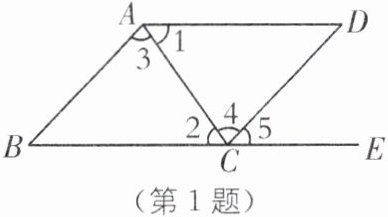
A.$\angle 1= \angle 2$
B.$\angle 3= \angle 4$
C.$\angle B+\angle BCD= 180^{\circ}$
D.$\angle B= \angle 5$
A
).
A.$\angle 1= \angle 2$
B.$\angle 3= \angle 4$
C.$\angle B+\angle BCD= 180^{\circ}$
D.$\angle B= \angle 5$
答案:A [解析]A.
∵∠1=∠2,
∴AD//BC,故本选项正确;
B.
∵∠3=∠4,
∴AB//CD,故本选项错误;
C.
∵∠B+∠BCD=180°,
∴AB//CD,故本选项错误;
D.
∵∠B=∠5,
∴AB//CD,故本选项错误.故选A
∵∠1=∠2,
∴AD//BC,故本选项正确;
B.
∵∠3=∠4,
∴AB//CD,故本选项错误;
C.
∵∠B+∠BCD=180°,
∴AB//CD,故本选项错误;
D.
∵∠B=∠5,
∴AB//CD,故本选项错误.故选A
2. (2025·泰州泰兴期末)如图,下列条件中,能判断$AD // BC$的是(

A.$\angle 1= \angle 3$
B.$\angle 2= \angle 4$
C.$\angle 1+\angle 4= 180^{\circ}$
D.$\angle 3+\angle 4= 180^{\circ}$
D
).
A.$\angle 1= \angle 3$
B.$\angle 2= \angle 4$
C.$\angle 1+\angle 4= 180^{\circ}$
D.$\angle 3+\angle 4= 180^{\circ}$
答案:D [解析]A.∠1=∠3,不能判定AD//BC,不符合题意;
B.∠2=∠4,不能判定AD//BC,不符合题意;
C.
∵∠1+∠4=180°,
∴AB//CD,不能判定AD//BC,不符合题意;
D.
∵∠3+∠4=180°,
∴AD//BC,符合题意.故选D.
B.∠2=∠4,不能判定AD//BC,不符合题意;
C.
∵∠1+∠4=180°,
∴AB//CD,不能判定AD//BC,不符合题意;
D.
∵∠3+∠4=180°,
∴AD//BC,符合题意.故选D.
3. (2025·福建漳州期中)如图所示,

在条件:①$\angle A = \angle ACE$;②$\angle B = \angle ACE$;③$\angle B = \angle ECD$;④$\angle B + \angle BCE = 180^{\circ}$中,能判定$AB // CE$的条件是______(填序号).

在条件:①$\angle A = \angle ACE$;②$\angle B = \angle ACE$;③$\angle B = \angle ECD$;④$\angle B + \angle BCE = 180^{\circ}$中,能判定$AB // CE$的条件是______(填序号).
①③④
答案:①③④ [解析]①由内错角相等,两直线平行判定AB//CE,故①符合题意;
②∠B和∠ACE不是同位角,也不是内错角,∠B=∠ACE不能判定AB//CE,故②不符合题意;
③由同位角相等,两直线平行判定AB//CE,故③符合题意;
④由同旁内角互补,两直线平行判定AB//CE,故④符合题意.
∴能判定AB//CE的条件是①③④.
②∠B和∠ACE不是同位角,也不是内错角,∠B=∠ACE不能判定AB//CE,故②不符合题意;
③由同位角相等,两直线平行判定AB//CE,故③符合题意;
④由同旁内角互补,两直线平行判定AB//CE,故④符合题意.
∴能判定AB//CE的条件是①③④.
4. M字型 如图,已知$BE$,$CE分别平分\angle ABC$,$\angle BCD$,且$\angle 1与\angle 2$互余,试说明$AB // CD$.


答案:
∵BE,CE分别平分∠ABC、∠BCD,
∴∠ABE=∠1,∠DCE=∠2.
∵∠1与∠2互余,
∴∠1+∠2=90°,
∴∠ABC+∠DCB=∠ABE+∠1+∠DCE+∠2=2∠1+2∠2=180°,
∴AB//CD.
∵BE,CE分别平分∠ABC、∠BCD,
∴∠ABE=∠1,∠DCE=∠2.
∵∠1与∠2互余,
∴∠1+∠2=90°,
∴∠ABC+∠DCB=∠ABE+∠1+∠DCE+∠2=2∠1+2∠2=180°,
∴AB//CD.
5. (2025·南京期末)如图,下列条件中:①$\angle 1= \angle C$;②$\angle 2= \angle C$;③$\angle BAC+\angle C= 180^{\circ}$;④$\angle ABE+\angle 2= 180^{\circ}$. 能判断$AB // CD$的有(

A.1个
B.2个
C.3个
D.4个
C
).
A.1个
B.2个
C.3个
D.4个
答案:C [解析]①由∠1=∠C能判定AB//CD,故①符合题意;②由∠2=∠C能判定AC//DE,不能判定AB//CD,故②不符合题意;③由∠BAC+∠C=180°能判定AB//CD,故③符合题意;④由对顶角的性质得到∠2和∠ABE的对顶角互补,能判定AB//CD,故④符合题意.故能判断AB//CD的有3个.故选C;
6. (2025·山西太原期末)将文具套尺中的量角器和三角板按照如图方式摆放. 其中,$\angle A= 30^{\circ}$,三角板的直角顶点$C$与量角器的中心重合,$DE$为量角器的直径. 下列条件中,不能判定$AB // DE$的是(

A.$\angle ACD= 30^{\circ}$
B.$\angle BCE= 60^{\circ}$
C.$\angle B+\angle BCD= 180^{\circ}$
D.$\angle BCE+\angle BCD= 180^{\circ}$
D
).
A.$\angle ACD= 30^{\circ}$
B.$\angle BCE= 60^{\circ}$
C.$\angle B+\angle BCD= 180^{\circ}$
D.$\angle BCE+\angle BCD= 180^{\circ}$
答案:D [解析]A.
∵∠A=30°,∠ACD=30°,
∴∠A=∠ACD,
∴AB//DE,不符合题意;
B.
∵∠A=30°,
∴∠B=90°−30°=60°.
∵∠BCE=60°,
∴∠B=∠BCE,
∴AB//DE,不符合题意;
C.
∵∠B+∠BCD=180°,
∴AB//DE,不符合题意;
D.∠BCE+∠BCD=180°,不能判定AB//DE,符合题意故选D.
∵∠A=30°,∠ACD=30°,
∴∠A=∠ACD,
∴AB//DE,不符合题意;
B.
∵∠A=30°,
∴∠B=90°−30°=60°.
∵∠BCE=60°,
∴∠B=∠BCE,
∴AB//DE,不符合题意;
C.
∵∠B+∠BCD=180°,
∴AB//DE,不符合题意;
D.∠BCE+∠BCD=180°,不能判定AB//DE,符合题意故选D.
7. 一副三角板按如图所示(共顶点$A$)叠放在一起,若固定三角板$ABC$,改变三角板$ADE$的位置(其中$A$点位置始终不变),当$\angle BAD= $______°时,$DE // AB$.


答案:
30或150 [解析]由题意,得∠ADE=30°,∠ACB=∠DAE=90°.
①如图
(1),当∠BAD=∠ADE=30°时,可得AB//DE;

②如图
(2),当∠BAD+∠D=180°时,可得AB//DE,则∠BAD=180°−∠D=150°.
30或150 [解析]由题意,得∠ADE=30°,∠ACB=∠DAE=90°.
①如图
(1),当∠BAD=∠ADE=30°时,可得AB//DE;

②如图
(2),当∠BAD+∠D=180°时,可得AB//DE,则∠BAD=180°−∠D=150°.
8. 分类讨论思想 (2025·镇江句容期末)如图,有一副直角三角板,$\angle ABC= \angle DBE= 90^{\circ}$,$\angle A= 60^{\circ}$,$\angle C= 30^{\circ}$,$\angle D= \angle E= 45^{\circ}$,现将三角板的直角顶点按照图中方式叠放,点$D在直线AB$上方,且$0^{\circ}<\angle ABD<180^{\circ}$,则能使三角板$ABC有一条边与DE平行的所有\angle ABD$的度数为______.


答案:
45°,165°,135° [解析]①如图
(1),当DE//AB时,
∴∠ABD=∠D=45°;
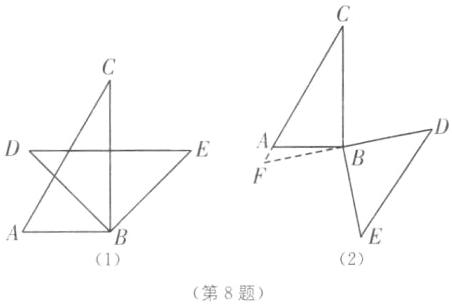
②如图
(2),当DE//AC时,延长DB交CA的延长线于点F,
∴∠F=∠D=45°,
∴∠ABF=15°,
∴∠ABD=180°−∠ABF=180°−15°=165°;
③如图
(3),当DE//BC时,
∴∠CBD=∠D=45°,
∴∠ABD=∠ABC+∠CBD=90°+45°=135°.

综上所述,使三角板ABC有一条边与DE平行的所有∠ABD的度数为45°,165°,135°.
45°,165°,135° [解析]①如图
(1),当DE//AB时,
∴∠ABD=∠D=45°;

②如图
(2),当DE//AC时,延长DB交CA的延长线于点F,
∴∠F=∠D=45°,
∴∠ABF=15°,
∴∠ABD=180°−∠ABF=180°−15°=165°;
③如图
(3),当DE//BC时,
∴∠CBD=∠D=45°,
∴∠ABD=∠ABC+∠CBD=90°+45°=135°.

综上所述,使三角板ABC有一条边与DE平行的所有∠ABD的度数为45°,165°,135°.