2024年6月25日14时7分,嫦娥六号携带月球背面样品成功返回地球,历时53天,38万千米的太空往返之旅,创造中国航天新的世界纪录.其中克服温差之大也是一大创举,月球表面的最高温度零上130℃,记作+130℃,最低温度零下180℃,应记作(
A.+1800℃
B.-180℃
C.+310℃
D.-310℃
B
).A.+1800℃
B.-180℃
C.+310℃
D.-310℃
答案:B
2.(2024·威海中考)一批食品,标准质量为每袋454 g.现随机抽取4个样品进行检测,把超过标准质量的克数用正数表示,不足的克数用负数表示.那么,最接近标准质量的是(
A.+7
B.-5
C.-3
D.10
C
).A.+7
B.-5
C.-3
D.10
答案:C
解析:
各选项与标准质量的偏差绝对值分别为:
$|+7|=7$,
$|-5|=5$,
$|-3|=3$,
$|10|=10$。
因为$3<5<7<10$,所以最接近标准质量的是选项C。
C
$|+7|=7$,
$|-5|=5$,
$|-3|=3$,
$|10|=10$。
因为$3<5<7<10$,所以最接近标准质量的是选项C。
C
3. 数轴上点A与数轴上表示3的点相距4个单位,则点A表示的数是(
A.-1或7
B.-1
C.7
D.1或-7
A
).A.-1或7
B.-1
C.7
D.1或-7
答案:A [解析]①当数轴上点A在数轴上表示3的点的左侧时,则点A表示的数是−1;②当数轴上点A在数轴上表示3的点的右侧时,则点A表示的数是7.综上所述,点A 表示的数是−1或7. 故选A
4. 如图(1),点A,B,C是数轴上从左到右排列的三个点,分别对应的数为-5,b,4,某同学将刻度尺如图(2)放置,使刻度尺上的数字0对齐数轴上的点A,发现点B对应刻度1.8 cm,点C对应刻度5.4 cm.则数轴上点B所对应的数b为(
A.3
B.-1
C.-2
D.-3
C
).A.3
B.-1
C.-2
D.-3
答案:C [解析]由题图
(1)可得AC=9,由题图
(2)可得AC=5.4cm,所以数轴上的一个单位长度对应刻度尺上的长度为5.4÷9=0.6(cm). 因为AB=1.8cm, 所以AB对应数轴的单位长度为1.8÷0.6=3, 所以在数轴上点B所对应的数b=−2. 故选C;
(1)可得AC=9,由题图
(2)可得AC=5.4cm,所以数轴上的一个单位长度对应刻度尺上的长度为5.4÷9=0.6(cm). 因为AB=1.8cm, 所以AB对应数轴的单位长度为1.8÷0.6=3, 所以在数轴上点B所对应的数b=−2. 故选C;
5. 分类讨论思想 若数轴上A,B两点之间的距离为8个单位长度,点A表示的有理数是-10,并且A,B两点经折叠后重合,此时折线与数轴的交点表示的有理数是(
A.-6
B.-9
C.-6或-14
D.-1或-9
C
).A.-6
B.-9
C.-6或-14
D.-1或-9
答案:C [解析]当点B在点A的左侧时,点B表示的有理数是−18,所以折线与数轴的交点表示的有理数是−14;当点B在点A的右侧时,点B表示的有理数是−2,所以折线与数轴的交点表示的有理数是−6. 故选C; 思路引导 本题考查了数轴以及有理数,分点B在点A 的左侧和点B在点A的右侧两种情况,找出点B表示的有理数是解题的关键.
6. 已知a>0,b<0,且|a|<|b|,则下列关系正确的是(
A.b<-a<a<-b
B.-a<b<a<-b
C.-a<b<-b<a
D.b<a<-b<-a
A
).A.b<-a<a<-b
B.-a<b<a<-b
C.-a<b<-b<a
D.b<a<-b<-a
答案:A [解析]因为a>0,b<0,|a|<|b|, 所以−a<0,−b>0,−a>b,−b>a, 所以b<−a<a<−b. 故选A 解后反思 本题主要考查了有理数大小比较的方法,解答本题的关键是要明确:①正数都大于0;②负数都小于0;③正数大于一切负数;④两个负数,绝对值大的负数小.
7. 已知0<x<1,请对x选取一个特殊的值:
(1)计算:$\frac{1}{x}$,-x,$-\frac{1}{x}$;
(2)比较x,-x,$\frac{1}{x}$,$-\frac{1}{x}$的大小,并用“<”把它们顺次连接起来.
(1)计算:$\frac{1}{x}$,-x,$-\frac{1}{x}$;
(2)比较x,-x,$\frac{1}{x}$,$-\frac{1}{x}$的大小,并用“<”把它们顺次连接起来.
答案:
(1)当x=$\frac{1}{2}$时,$\frac{1}{x}$=2,−x=−$\frac{1}{2}$,−$\frac{1}{x}$=−2(x取值不唯一).
(2)−$\frac{1}{x}$<−x<x<$\frac{1}{x}$.
(1)当x=$\frac{1}{2}$时,$\frac{1}{x}$=2,−x=−$\frac{1}{2}$,−$\frac{1}{x}$=−2(x取值不唯一).
(2)−$\frac{1}{x}$<−x<x<$\frac{1}{x}$.
8. 等边三角形ABC在数轴上的位置如图所示,点A,C对应的数分别为0和-1,若△ABC绕顶点沿顺时针方向在数轴上连续翻转,翻转1次后,点B所对应的数为1,则连续翻转2025次后,则数2025对应的点为(
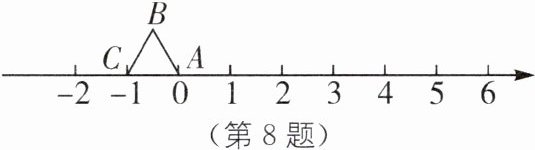
A.点A
B.点B
C.点C
D.不能确定
A
).
A.点A
B.点B
C.点C
D.不能确定
答案:A [解析]因为翻转1次后,数1对应的点为B,翻转2次后,数2对应的点为C,翻转3次后,数3对应的点为A,翻转4次后,数4对应的点为B,...,所以点的变化周期为3.又2025÷3=675,所以连续翻转2025次后,数2025对应的点为A. 故选A.