1. (2025·浙江杭州滨江区期中)下列交换加数位置的变形,正确的是(
A.$-3 + 4 - 3 = -3 + 3 - 4$
B.$-3 + 4 - 3 = -4 + 3 - 3$
C.$\frac{6}{7} + 1.5 - \frac{1}{7} = \frac{6}{7} - \frac{1}{7} + 1.5$
D.$\frac{6}{7} + 1.5 - \frac{1}{7} = \frac{6}{7} - \frac{1}{7} - 1.5$
C
).A.$-3 + 4 - 3 = -3 + 3 - 4$
B.$-3 + 4 - 3 = -4 + 3 - 3$
C.$\frac{6}{7} + 1.5 - \frac{1}{7} = \frac{6}{7} - \frac{1}{7} + 1.5$
D.$\frac{6}{7} + 1.5 - \frac{1}{7} = \frac{6}{7} - \frac{1}{7} - 1.5$
答案：C
2. (2025·河北石家庄裕华区期末)小明同学在解题时,将式子$-\frac{1}{3} + \frac{2}{5} + (-\frac{2}{3}) - (-\frac{3}{5})$变成$[-\frac{1}{3} + (-\frac{2}{3})] + [\frac{2}{5} - (-\frac{3}{5})]$后再进行计算,该同学运用了(
A.加法交换律
B.加法结合律
C.加法交换律和结合律
D.分配律
C
).A.加法交换律
B.加法结合律
C.加法交换律和结合律
D.分配律
答案：C
解析：
原式$-\frac{1}{3} + \frac{2}{5} + (-\frac{2}{3}) - (-\frac{3}{5})$变为$[-\frac{1}{3} + (-\frac{2}{3})] + [\frac{2}{5} - (-\frac{3}{5})]$，先交换了$\frac{2}{5}$与$-\frac{2}{3}$的位置，运用了加法交换律；再将$-\frac{1}{3}$与$-\frac{2}{3}$结合、$\frac{2}{5}$与$-(-\frac{3}{5})$结合，运用了加法结合律。
C
C
3. 上午 10:00 的气温为$18^{\circ}C$,到中午 12:00 气温上升了$4^{\circ}C$,到晚上 6:00 气温又下降了$9^{\circ}C$,则晚上 6:00 的气温是
13
$^{\circ}C$.答案：13
解析：
18 + 4 - 9 = 13
4. 教材 P39 例 5·变式 (2024·徐州期中)计算：
(1)$-12 - (-18) + (-7)$；
(2)$(-1\frac{1}{2}) + 1.25 + (-8.5) + 10\frac{3}{4}$.
(1)$-12 - (-18) + (-7)$；
(2)$(-1\frac{1}{2}) + 1.25 + (-8.5) + 10\frac{3}{4}$.
答案：
(1)原式=-12+18-7=-1；
(2)原式=-1.5+(-8.5)+(1.25+10.75)=-10+12=2.
(1)原式=-12+18-7=-1；
(2)原式=-1.5+(-8.5)+(1.25+10.75)=-10+12=2.
5. 小嘉全班在操场上围坐成一圈. 若以班长为第 1 人,依顺时针方向算人数,小嘉是第 17 人；若以班长为第 1 人,依逆时针方向算人数,小嘉是第 21 人. 则小嘉班上共有(
A.36 人
B.37 人
C.38 人
D.39 人
A
).A.36 人
B.37 人
C.38 人
D.39 人
答案：A [解析]根据题意知,小嘉和班长两次都数了，所以班上共有17+21-2=36(人).故选A.
6. (广西南宁三中自主招生)某中学派 40 名学生参加运动会,其中得金牌的 12 人,得银牌的 5 人,得铜牌的 8 人,同时得金、银牌的 2 人,同时得金、铜牌的 6 人,同时得银、铜牌的 3 人,同时得金、银、铜牌的 1 人,那么这所中学派出的学生中没有得奖牌的有
25
人.答案：25 [解析]40-(12+5+8-2-6-3+1)=40-15=25(人).故这所中学派出的学生中没有得奖牌的有25人.思路引导 本题主要考查了有理数的加减混合运算，解答本题的关键是要明确:这所中学派出的学生中得奖牌的人数=得金牌的人数+得银牌的人数+得铜牌的人数-同时得金、银牌的人数-同时得金、铜牌的人数-同时得银、铜牌的人数+同时得金、银、铜牌的人数.
解析：
得奖牌的人数为：$12 + 5 + 8 - 2 - 6 - 3 + 1$
$=17 + 8 - 2 - 6 - 3 + 1$
$=25 - 2 - 6 - 3 + 1$
$=23 - 6 - 3 + 1$
$=17 - 3 + 1$
$=14 + 1$
$=15$（人）
没有得奖牌的人数为：$40 - 15 = 25$（人）
25
$=17 + 8 - 2 - 6 - 3 + 1$
$=25 - 2 - 6 - 3 + 1$
$=23 - 6 - 3 + 1$
$=17 - 3 + 1$
$=14 + 1$
$=15$（人）
没有得奖牌的人数为：$40 - 15 = 25$（人）
25
$7. $分类讨论思想$ $在有理数的范围内$,$我们定义三个数之间的新运算$“”$法则：如：
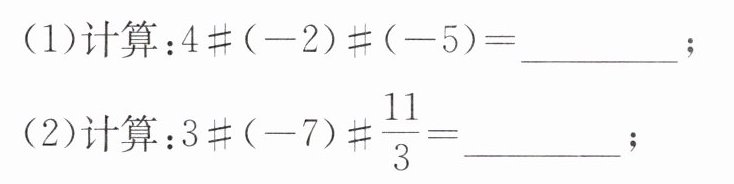
$(3)$在$-\frac{6}{7},-\frac{5}{7},…,-\frac{1}{7},0,\frac{1}{9},\frac{2}{9},…,\frac{8}{9}$这$ 15 $个数中：$①$任取三个数作为$a,b,c$的值$,$进行运算$,$则所有计算结果的最小值是______；$②$若将这$ 15 $个数任意分成$ 5 $组$,$每组三个数$,$进行运算$,$得到$ 5 $个不同的结果$,$由于分组不同$,$所以$ 5 $个运算的结果也不同$,$那么$ 5 $个结果之和的最大值是______.
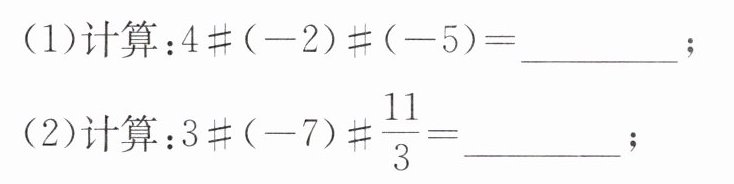
$(3)$在$-\frac{6}{7},-\frac{5}{7},…,-\frac{1}{7},0,\frac{1}{9},\frac{2}{9},…,\frac{8}{9}$这$ 15 $个数中：$①$任取三个数作为$a,b,c$的值$,$进行运算$,$则所有计算结果的最小值是______；$②$若将这$ 15 $个数任意分成$ 5 $组$,$每组三个数$,$进行运算$,$得到$ 5 $个不同的结果$,$由于分组不同$,$所以$ 5 $个运算的结果也不同$,$那么$ 5 $个结果之和的最大值是______.
答案：
(1)4
(2)3
(3)①$-\frac{6}{7}$ [解析]分两种情况:当$a\geqslant b+c$时，$a\#b\#c=\frac{a-b-c+a+b+c}{2}=a$，当$a\geqslant b+c$时，$|a-b-c|\geqslant 0$ 当a最小，即$a=-\frac{6}{7}$时，有最小值$-\frac{6}{7}$;当$a\lt b+c$时，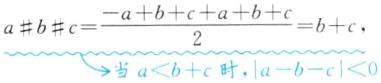
当$b+c$最小时，$a\#b\#c$的值最小.因为$a\lt b+c$，所以$a=-\frac{6}{7}$，$b+c$的最小值为$-\frac{5}{7}$，$-\frac{6}{7}\lt -\frac{5}{7}$.故在“$a\#b\#c$”运算中，所有计算结果的最小值是$-\frac{6}{7}$. ②4 [解析]因为当$a=-\frac{6}{7}$，$b=\frac{1}{9}$，$c=\frac{2}{9}$时，原式$=\frac{1}{9}+\frac{2}{9}=\frac{1}{3}$；当$a=-\frac{5}{7}$，$b=\frac{1}{3}$，$c=\frac{4}{9}$时，原式$=\frac{1}{3}+\frac{4}{9}=\frac{7}{9}$；当$a=-\frac{4}{7}$，$b=\frac{5}{9}$，$c=\frac{2}{3}$时，原式$=\frac{5}{9}+\frac{2}{3}=\frac{11}{9}$；当$a=-\frac{3}{7}$，$b=\frac{7}{9}$，$c=\frac{8}{9}$时，原式$=\frac{7}{9}+\frac{8}{9}=\frac{5}{3}$；当$a=0$，$b=-\frac{1}{7}$，$c=-\frac{2}{7}$时，原式=0，所以五个结果之和的最大值为$\frac{1}{3}+\frac{7}{9}+\frac{11}{9}+\frac{5}{3}=4$.
(1)4
(2)3
(3)①$-\frac{6}{7}$ [解析]分两种情况:当$a\geqslant b+c$时，$a\#b\#c=\frac{a-b-c+a+b+c}{2}=a$，当$a\geqslant b+c$时，$|a-b-c|\geqslant 0$ 当a最小，即$a=-\frac{6}{7}$时，有最小值$-\frac{6}{7}$;当$a\lt b+c$时，
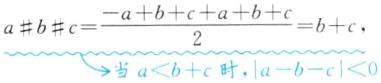当$b+c$最小时，$a\#b\#c$的值最小.因为$a\lt b+c$，所以$a=-\frac{6}{7}$，$b+c$的最小值为$-\frac{5}{7}$，$-\frac{6}{7}\lt -\frac{5}{7}$.故在“$a\#b\#c$”运算中，所有计算结果的最小值是$-\frac{6}{7}$. ②4 [解析]因为当$a=-\frac{6}{7}$，$b=\frac{1}{9}$，$c=\frac{2}{9}$时，原式$=\frac{1}{9}+\frac{2}{9}=\frac{1}{3}$；当$a=-\frac{5}{7}$，$b=\frac{1}{3}$，$c=\frac{4}{9}$时，原式$=\frac{1}{3}+\frac{4}{9}=\frac{7}{9}$；当$a=-\frac{4}{7}$，$b=\frac{5}{9}$，$c=\frac{2}{3}$时，原式$=\frac{5}{9}+\frac{2}{3}=\frac{11}{9}$；当$a=-\frac{3}{7}$，$b=\frac{7}{9}$，$c=\frac{8}{9}$时，原式$=\frac{7}{9}+\frac{8}{9}=\frac{5}{3}$；当$a=0$，$b=-\frac{1}{7}$，$c=-\frac{2}{7}$时，原式=0，所以五个结果之和的最大值为$\frac{1}{3}+\frac{7}{9}+\frac{11}{9}+\frac{5}{3}=4$.